Նեյրոնային ցանցեր և խորը ուսուցում
Խնդիրների և վարժությունների մասին
 Ձեռագիր թվանշանների ճանաչում՝ օգտագործելով նեյրոնային ցանցեր
Ձեռագիր թվանշանների ճանաչում՝ օգտագործելով նեյրոնային ցանցեր
 Ինչպե՞ս է աշխատում հետադարձ տարածումը
Ինչպե՞ս է աշխատում հետադարձ տարածումը
 Նեյրոնային ցանցերի ուսուցման բարելավումը
Նեյրոնային ցանցերի ուսուցման բարելավումը
 Տեսողական ապացույց այն մասին, որ նեյրոնային ֆունկցիաները կարող են մոտարկել կամայական ֆունկցիա
Տեսողական ապացույց այն մասին, որ նեյրոնային ֆունկցիաները կարող են մոտարկել կամայական ֆունկցիա
 Ինչու՞մն է կայանում նեյրոնային ցանցերի մարզման բարդությունը
Ինչու՞մն է կայանում նեյրոնային ցանցերի մարզման բարդությունը
Հավելված: Արդյո՞ք գոյություն ունի ինտելեկտի պարզ ալգորիթմ





Նախորդ գլխում տեսանք, թե ինչպես նեյրոնային ցանցերը կարող են գրադիենտային վայրէջքի օգնությամբ սովորել իրենց կշիռներն ու շեղումները։ Սակայն մեր բացատրություններում բաց թողում կար, այն է՝ ինչպե՞ս հաշվել գնի ֆունկցիայի գրադիենտը։ Դա էական բացթողում է։ Այս գլխում կդիտարկենք գրադիենտների հաշվման արագագործ ալգորիթմ, որի անունն է հետադարձ տարածում (backpropagation)։
Հետադարձ տարածման ալգորիթմի նկարագրությունն առաջին անգամ հանդիպել է 1970-ականներին, սակայն իր կարևորությունն ամբողջապես չի գնահատվել մինչ 1986 թվականի այս հոդվածը՝ հեղինակված Դավիթ Ռումելհարթի, Ջոֆֆրի Հինթոնի և Ռոնալդ Վիլյամսի կոմից։ Այդ հոդվածը նկարագրում է մի քանի նեյրոնային ցանցեր, որտեղ հետադարձ տարածումն աշխատում է շատ ավելի արագ, քան ավելի վաղ ժամանակներում օգտագործվող ուսուցման մեթոդները, այդպիսով, հնարավոր է դարձնում նեյրոնային ցանցերի օգտագործումը նախկինում անլուծելի խնդիրների լուծման նպատակով Այսօր հետադարձ տարածումը նեյրոնային ցանցերով ուսուցման հիմնական շարժիչ ուժն է։
Այս գլխում ավելի շատ են զետեղված մաթեմատիկական դուրսբերումներ, քան մնացած այլ գլուխներում։ Եթե դուք հրապուրված չեք մաթեմատիկայով, ապա կարող եք այս գլուխը բաց թողնել և հետադարձ տարածումն ընկալել որպես «սև արկղ», որի մանրամասները գիտակցաբար անտեսում եք։ Սակայն ինչու՞ ժամանակ ծախսել և այդ մանրամասները սովորել։
Պատճառն, իհարկե, խորությամբ հասկանալու ձգտումն է։ Հետադարձ տարածման հիմքում ընկած է $C$ գնի ֆունկցիայի՝ նեյրոնային ցանցերի $w$ կշիռների (կամ $b$ շեղումների) նկատմամբ մասնակի ածանցյալի $\partial C / \partial w$ արտահայտությունը։ Այն ցույց է տալիս, թե ինչ «արագությամբ» է գինը փոփոխվում՝ կախված կշիռների և շեղումների փոփոխությունից։ Այս արտահայտությունը փոքր-ինչ բարդ տեսք ունի, սակայն այն միաժամանակ շատ գեղեցիկ է, որի յուրաքանչյուր մասնիկն ունի բնական, ինտուիտիվ բացատրություն։ Եվ, այսպիսով, հետադարձ տարածումը միայն արագագործ ալգորիթմ չէ, որը «ստիպված» ենք սովորել։ Իրականում այն տալիս է խորը ներըմբռնում (insight) այն մասին, թե ինչպես է կշիռների և շեղումների փոփոխությունն ազդում ցանցի վարքագծի վրա։ Այդ իսկ պատճառով այս ալգորիթմն արժանի է մանրամասն ուսուցման։
Այսպիսով, եթե ցանկություն ունեք թռուցիկ կարդալ կամ ուղղակի ցատկել հեջորդ գլխին, ապա դա նորմալ է։ Գրքի շարունակությունն այնպես է շարադրված, որ այն հասանելի է անգամ եթե դուք հետադարձ տարածումը դիտարկեք որպես սև արկղ։ Իհարկե, ավելի ուշ, գրքում կան կետեր, որոնք հղվում են այս գլխի արդյունքներին, սակայն այդ կետերում սպասվում է, որ դուք կկարողանաք հասկանալ հիմնական եզրահանգումները անգամ եթե չեք հետևել ամբողջական տրամաբանությանը։
Մարզանք. նեյրոնային ցանցի ելքային արժեքների հաշվման արագագործ, մատրիցային մոտեցում
Մինչ հետադարձ տարածումը քննարկելը, որպես նախավարժանք դիտարկենք նեյրոնային ցանցի ելքային արժեքը հաշվելու արագագործ մատրիցային ալգորիթմ։ Իրականում մենք այդ ալգորիթմը համառոտ կերպով հանդիպել ենք նախորդ գլխի վերջնահատվածում, սակայն այն քննարկեցինք արագորեն, հետևաբար կվերադառնանք և ավելի մանրամասն կդիտարկենք այս բաժնում։ Հատկապես, դա հնարավորություն կտա մեզ ծանոթանալ այն նշանակումներին, որոնք օգտագործվում են հետադարձ տարածման մեջ՝ արդեն հայտնի համատեքստում։
Նախ ցանցի կշիռներին տանք այնպիսի նշանակումներ, որոնք կօգտագործենք այդ կշիռներին հստակորեն հղվելու նպատակով։ Նշանակենք $w^l_{jk}$-ով ցանցի $(l-1)^{\rm րդ}$ շերտի $k^{\rm րդ}$ նեյրոնը $l^{\rm րդ}$ շերտի $j^{\rm րդ}$ նեյրոնին միացնող կապի կշիռը։ Այսպիսով, օրինակ, ներքևի դիագրամում պատկերված կշիռը երկրորդ շերտի չորրորդ նեյրոնը միացնում է երրորդ շերտի երկրորդ նեյրոնի հետ.
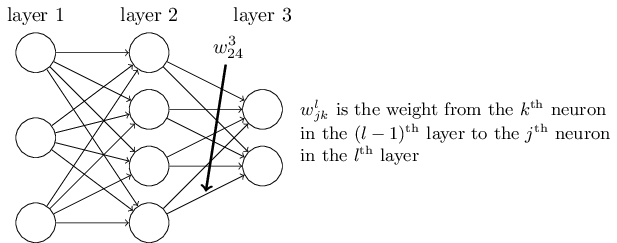
Նմանատիպ նշանակումներ են օգտագործվում նաև ցանցի շեղումների և ակտիվացիաների համար։ Եվ այսպես, $l^{\rm րդ}$ շերտի $j^{\rm րդ}$ նեյրոնին համապատասխանող շեղումը կնշանակենք $b^l_j$-ով։ Ստորև ներկայացված դիագրամը ցույց է տալիս, թե ինչպես օգտագործել այս նշանակումները.
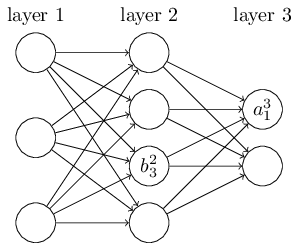
Այսպիսով, (23) հավասարումն արտագրենք մատրիցային տեսքով, որի հիմքում ընկած է արդեն քննարկված ֆունկցիաների վեկտորացման գաղափարը։ Մեր նպատակն է, որպեսի $\sigma$-ն կարողանանք կիրառել $v$ վեկտորի բոլոր էլեմենտների վրա։ Ֆունկցիայի էլեմենտ-առ-էլեմենտ կիրառումը նշանակենք $\sigma(v)$ արտահայտությամբ։ $\sigma(v)$-ի տարրերը պարզապես $\sigma(v)_j = \sigma(v_j)$ էլեմենտներն են։ Որպես օրինակ, դիտարկենք այն դեպքը, երբ ունենք $f(x) = x^2$ ֆունկցիան, ապա ֆունկցիայի վեկտորացված տեսքը կլինի՝ \begin{eqnarray} f\left(\left[ \begin{array}{c} 2 \\ 3 \end{array} \right] \right) = \left[ \begin{array}{c} f(2) \\ f(3) \end{array} \right] = \left[ \begin{array}{c} 4 \\ 9 \end{array} \right], \tag{24}\end{eqnarray} այսինքն վեկտորացված $f$-ն ուղղակի վեկտորի յուաքանչյուր անդամը քառակուսի է բարձրացնում։
Հաշվի առնելով այս բոլոր նշանակումները, (23) հավասարումը կարելի է արտագրել այսպիսի գեղեցիկ և կոմպակտ վեկտորացված տեսքով. \begin{eqnarray} a^{l} = \sigma(w^l a^{l-1}+b^l). \tag{25}\end{eqnarray} Այս արտահայտությունը ընդհանուր առմամբ հնարավորություն է տալիս դիտարկել նախորդ շերտի ակտիվացիաների ազդեցությունը հաջորդ շերտի ակտիվացիաների վրա. ուղղակի կիրառում ենք կշիռների մատրիցը ակտիվացիաների վրա, այնուհետև ավելացնում ենք շեղման վեկտորը և վերջապես կիրառում $\sigma$ ֆունկցիան * *Ի դեպ, այս արտահայտությունն է, որ մոտիվացնում է $w^l_{jk}$ նշանակման ինդեքսների «տարօրինակ» հաջորդականությունը։ Եթե մենք օգտագործեինք $j$ ինդեքսը մուտքային նեյրոնի համար և $k$-ն ելքային նեյրոնի համար, ապա ստիպված կլինեինք (25) հավասարման մեջ կշիռների մատրիցը փոխարինել տրանսպոնացված մատրիցով։ Դա փոքր փոփոխություն է, բայց դժվարություններ առաջացնող և մենք կկորցնեինք այն պարզ մտավոր մոդելը, որը թույլ է տալիս օգտագործել «կշիռների մատրիցը կիրառենք ակտիվացիաների վրա» արտահայտությունը։։ Այսպիսի գլոբալ տեսքը հաճախ ավելի հեշտ է ընկալել և ավելի հակիրճ է (և պարունակում է ավելի քիչ ինդեքսներ) քան նեյրոն-առ-նեյրոն տեսքը, որը մենք դիտարկում էինք մինչ այժմ։ Դա ինդեքսային դժողքից խուսափելու մեխանիզմ է, որը միաժամանակ հստակություն է ապահովում այն առումով, թե առհասարակ ինչի մասին է գնում խոսքը։ Արտահայտությունն օգտակար է նաև պրակտիկ տեսանկյունից, քանի որ մատրիցային գրադարանների մեծ մասն ապահովում են մատրիցային բազմապատկման, վեկտորների գումարման և վեկտորացման արագագործ իրականացումներ։ Նախորդ գլխում զետեղված կոդը անուղղակիորեն օգտագործեց այս արատահայտությունը, որպեսզի հաշվարկի ցանցի վարքագիծը։
Երբ (25) հավասարումն օգտագործում ենք $a^l$-ը հաշվելու նպատակով, ապա հաշվում ենք նաև միջանկյալ $z^l \equiv w^l a^{l-1}+b^l$ արժեքը։ Այդ մեծությունը նշանակենք որպես $z^l$ ՝ $l$-րդ շերտի նեյրոնների կշռված մուտքեր (weighted input)։ Հետագայում այս գլխում նաև կտեսնեք $z^l$ կշռված մուտքերի կիրառությունը։ (25) հավասարումը երբեմն արտահայտվում է կշռված մուտքերի միջոցով՝ $a^l = \sigma(z^l)$։ Հարկ է նշել նաև, որ $z^l$-ի տարրերը $z^l_j = \sum_k w^l_{jk} a^{l-1}_k+b^l_j$ կամ պարզապես $z^l_j$-ը $l$-րդ շերտի $j$-րդ նեյրոնի ակտիվացիայի ֆունկցիայի կշռված մուտքն է։
Երկու ենթադրություններ գնային ֆունկցիայի վերաբերյալ
Հետադարձ տարածման նպատակն է հաշվել $C$ գնային ֆունկցիայի $\partial C / \partial w$ և $\partial C / \partial b$ մասնական ածանցյալները $w$ կշիռների և $b$ շեղումների նկատմամբ։ Կատարենք երկու ենթադրություններ հետադարձ տարածման համար։ Սակայն, մինչ այդ դիտարկենք քառակուսային գնային ֆունկցիան՝ սահմանված նախորդ գլխում (տես (6) հավասարումը)։ Նախորդ գլխից հայտնի է, որ քառակուսային գնային ֆունկցիան ունի հետևյալ տեսքը՝ \begin{eqnarray} C = \frac{1}{2n} \sum_x \|y(x)-a^L(x)\|^2, \tag{26}\end{eqnarray} որտեղ $n$-ը մարզման օրինակների քանակն է, իսկ գումարն ըստ անհատական $x$ մարզման օրինակների է, $y = y(x)$ համապատասխան ցանկալի ելքային արժեքն է և $a^L = a^L(x)$ ցանցի ելքային վեկտորն է $x$ մուտքային վեկտորի դեպքում։
Այպիսով, ի՞նչ ենթադրություններ կարող ենք կատարել $C$ գնային ֆունկցիայի վերաբերյալ, որպեսզի հետադարձ տարածումը հնարավոր լինի կիրառել։ Առաջին ենտադրությունն այն է, որ գնային ֆունկցիան կարելի է արտահայտել $C = \frac{1}{n} \sum_x C_x$ հավասարմամբ որպես $x$ մարզման օրինակներից կախված առանձին $C_x$ գնային ֆունկցիաների հանրահաշվական միջին։ Այս պնդումը ճիշտ է քառակուսային գնային ֆունկցիայի դեպքում, որտեղ $C_x = \frac{1}{2} \|y-a^L \|^2$ գնային ֆունկցիան է՝ կախված մեկ մարզման օրինակից։ Այս ենթադրությունը ճիշտ կլինի նաև մնացած այլ գնային ֆունկցիաների դեպքում, որ կհանդիպենք այս գրքում։
Մենք այս ենթադրության կարիքն ունենք, քանի որ հետադարձ տարածումն, ըստ էության, մեզ հնարավորություն է տալիս հաշվել $\partial C_x / \partial w$ և $\partial C_x / \partial b$ մասկանակն ածանցյալները մեկ մարզման օրինակի համար։ Այնուհետև $\partial C / \partial w$ և $\partial C / \partial b$ արժեքները կվերականգնենք՝ հաշվելով միջինը բոլոր մարզման օրինակների երկայնքով։ Այսպիսով, հաշվի առնելով վերևում կատարված պնդումը, կարող ենք $C_x$ գնային ֆունկցիայի $x$ ինդեքսը դեն նետել և գնային ֆունկցյաին հղվել որպես $C$, քանի որ մասնական ածանցյալի դիտարկումը բերվեց ֆիքսված մուտքային վեկտորի դեպքում մասնական ածանցյալի հաշվմանը։ Վերջ ի վերջո $x$ ինդեքսը հետ կբերենք, սակայն նշանակումների պարզության համար այն առայժմ բաց կթողնենք։
Գնային ֆունկցիայի մասին երկրորդ ենթադրությունը այն է, որ այն կարելի է արտահայտել որպես ֆունկցիա կախված նեյրոնային ցանցերի ելքային արժեքներից.
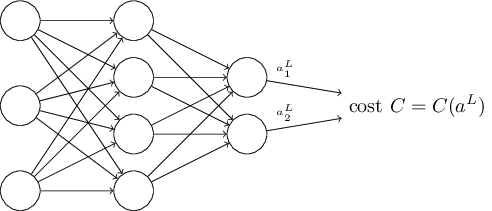
Հադամարի արտադրյալը՝ $s \odot t$
Հետադարձ տարածման ալգորիթմը հիմնված է որոշ գծային հանրահաշվի գործողությունների վրա՝ վեկտորների գումարում, վեկտորի բազմապատկում մատրիցով և այլն։ Սակայն գործողություններից մեկն ավելի քիչ հաճախ է օգտագործվում քան մնացածները։ Ենթադրենք, որ $s$ և $t$ միևնույն չափողականությամբ վեկտորներ են։ Վեկտորների էլեմենտ առ էլեմենտ արտադրյալը նշանակենք $s \odot t$ արտահայտությամբ։ Հետևաբար $s \odot t$ արտադրյալի տարրերը կլինեն $(s \odot t)_j = s_j t_j$ արժեքները։ Դիտարկենք հետևյալ օրինակը. \begin{eqnarray} \left[\begin{array}{c} 1 \\ 2 \end{array}\right] \odot \left[\begin{array}{c} 3 \\ 4\end{array} \right] = \left[ \begin{array}{c} 1 * 3 \\ 2 * 4 \end{array} \right] = \left[ \begin{array}{c} 3 \\ 8 \end{array} \right]. \tag{28}\end{eqnarray} Այս էլեմենտ առ էլեմենտ արտադրյալը այլ կերպ անվանում են Հադամարի արտադրյալ կամ Շուրի արտադրյալ։ Մենք կօգտագործենք Հադամարի արտադրյալ տերմինը։ Լավ մատրիցային գրադարանները սովորաբար տրամադրում են արագագործ Հադամարի արտադրյալի իրականացում, որը բավականին օգտակար է հետադարձ տարածումն իրականացնելիս։
Հետադարձ տարածման հիմքում ընկած չորս հիմնական հավասարումները
Հետադարձ տարածումն այն մասին է, թե ինչպես է ցանցի գնային ֆունկցիան փոփոխվում՝ կախված կշիռների և շեղումների փոփոխություններից։ Սա իր հերթին նշանակում է, որ պետք է հաշվել $\partial C / \partial w^l_{jk}$ և $\partial C / \partial b^l_j$ մասնակի ածանցյալները։ Նախ ներմուծենք $\delta^l_j$ միջանկյալ մեծությունը, որը կկոչենք $l^{\rm րդ}$ շերտի $j^{\rm րդ}$ նեյրոնի սխալանք (error)։ Հետադարձ տարածումը ցույց կտա որոշակի պրոցեդուրա $\delta^l_j$ սխալանքը հաշվելու համար, այնուհետև $\delta^l_j$-ն կկապենք $\partial C / \partial w^l_{jk}$ և $\partial C / \partial b^l_j$ մասնակի ածանցյալների հետ։
Որպեսզի հասկանանք, թե ինչպես է սխալանքը սահմանումը, պատկերացնենք, որ մեր նեյրոնային ցանցում սատանա է հայտնվել։

Հարկ է նշել, որ այդ սատանան ունի բարի նպատակներ և փորձում է օգնել ձեզ գինը բարելավել, օրինակ, գտնել այնպիսի $\Delta z^l_j$, որի արդյունքում գինը կնվազի։ Ենթադրենք $\frac{\partial C}{\partial z^l_j}$ մասնակի ածանցյալն ունի բավականին մեծ արժեք (դրական կամ բացասական)։ Սատանան կարող է բավականին իջեցնել գինը, ընտրելով այնպիսի $\Delta z^l_j$, որը հակառակ նշանի է $\frac{\partial C}{\partial z^l_j}$ մեծության նկատմամբ։ Ընդ որում, եթե $\frac{\partial C}{\partial z^l_j}$ մոտ է զրոյին, ապա սատանան էապես չի կարող ազդել գնի բարելավման հարցում՝ «խառնաշփոթ» առաջացնելով $z^l_j$ կշռված մուտքին։ Եվ այդ դեպքում սատանան կհանգի այն եզրակացության, որ նեյրոնն արդեն մոտ է օպտիմալ լինելուն* * Սա ճիշտ է միայն փոքր $\Delta z^l_j$ փոփոխությունների դեպքում, իհարկե։ Մենք կենթադրենք, որ սատանան սահմանափակված է այդպիսի փոքր փոփոխություններ անելուն։ ։ Այսպիսով, ինտուիտիվ կարելի է հասկանալ, որ $\frac{\partial C}{\partial z^l_j}$ մասնակի ածանցյալը նեյրոնում առկա սխալանքի համար որոշակի չափ է հանդիսանում։
Այս պատմությունը ոգեշնչում է, որպեսզի $l$-րդ շերտի $j$-րդ նեյրոնի $\delta^l_j$ սխալանքը սահմանենք որպես \begin{eqnarray} \delta^l_j \equiv \frac{\partial C}{\partial z^l_j}. \tag{29}\end{eqnarray} Ինչպես մնացած դեպքերում, $\delta^l$-ով կնշանակենք $l$-րդ շերտի սխալանքների վեկտորը։ Հետադարձ տարածումը մեզ հնարավորություն կտա, որպեսզի բոլոր շերտերի համար հաշվենք $\delta^l$ մեծությունը, այնուհետև այդ սխալանքները կապենք այն արժեքների հետ, որոնք իրապես մեր հետաքրքրությունների շրջանակներիում են՝ $\partial C / \partial w^l_{jk}$ և $\partial C / \partial b^l_j$։
Հարց է առաջանում, թե ինչու է սատանան փոփոխում $z^l_j$ կշռված մուտքի արժեքը։ Բնական կլիներ, որ սատանան փոփոխեր $a^l_j$ ակտիվացիայի արժեքը, ինչի արդյունքում $\frac{\partial C}{\partial a^l_j}$ մեծությունը կօգտագործեինք սխալանքը չափելու նպատակով։ Ըստ էության, եթե այդ ուղղությամբ գնանք, ապա կստանանք նպանատիպ արդյունք, որը նկարագրված է ներքևում։ Սակայն տարբերությունն այն է, որ այս մոտեցման դեպքում հետադարձ տարածման մաթեմատիկական ներկայացումն ավելի բարդ տեսք ունի։ Հետևաբար կաշխատենք $\delta^l_j = \frac{\partial C}{\partial z^l_j}$ մեծության հետ որպես սխալանքի չափման գործիք* * Այնպիսի դասակարգման խնդիրներում, ինչպիսին է MNIST-ը, «սխալանք» տերմինը սովորաբար օգտագործվում է դասակարգման ձախողման գործակցի իմաստով։ Օրինակ, երբ նեյրոնային ցանցը թվանշանների 96.0 տոկոսը ճիշտ է դասակարգում, ապա ձախողման գործակիցը 4.0 տոկոս է։ Իհարկե, $\delta$ վեկտորների իմաստը փոքր-ինչ այլ է, սակայն պրակտիկորեն դժվար չի լինի հասկանալ իմաստների տարբերությունը կախված կոնտեքստից։ ։
Հարձակման պլանը։ Հետադարձ տարածումը հիմնված է 4 ֆունդամենտալ հավասարումների վրա։ Այդ հավասարումները միասին մեզ հնարավորություն են տալիս հաշվել $\delta^l$ սխալանքն ու գնային ֆունկցիայի գրադիենտը։ 4 հավասարումները կնկարագրենք ավելի ուշ, սակայն պետք չէ սպասել, որ անմիջապես հեշտությամբ կընկալեք, հակառակ դեպքում կարող է հիասթափություն ապրեք։ Ըստ էության, հետադարձ տարածման հավասարումներն այնքան հարուստ են, որ իրենց լավ հասկանալու համար կպահանջվի բավականին ժամանակ և համբերություն՝ աստիճանաբար ավելի խորանալու համար։ Լավ նորությունն այն է, որ այդպիսի համբերատարությունը բազմակատիկ վարձատրվում է։ Եվ այսպիսով, քննարկումներն այս բաժնում միայն սկիզբն են, որպեսզի օգնեն խորությամբ հասկանալ և ճանապարհը հարթեն։
Ահա նախադիտում (preview) այն մասին, թե ինչպես այս գլխում կխորանանք հավասարումների մեջ։ Ես կտամ հավասարումներին կարճ ապացույցներ , որ կօգնի բացատրել, թե ինչու իրենք տեղի ունեն։ Այնուհետև մենք կվերաձևակերպենք հավասարումները ալգորիթմական տեսքով որպես պսեվդոկոդ և կտեսնենք, թե ինչպես կարելի է պսեվդոկոդն իրականացնել որպես աշխատող Python կոդ։ Գլխի վերջնական բաժնում կկառուցենք հետադարձ տարածման հավասարումների ինտուիտիվ պատկերացում և կխոսենք այն մասին, թե ինչպես կարելի էր զրոյից հայտնագործել իրենց։ Ամբողջ ընթացքում շարունակաբար կվերադառնանք այդ չորս հիմնական հավասարումներին և ավելի խորը հասկանալուն զուգընթաց հավասարումներն ավելի հարմարավետ կդառնան, և, հնարավոր է, որ նույնիսկ գեղեցիկ և բնական։
Ելքային շերտի սխալանքի $\delta^L$ հավասարումը։ $\delta^L$ հավասարման էլեմենտներն ունեն հետևյալ տեսքը՝ \begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j). \tag{BP1}\end{eqnarray} Դիտարկենք այդ արտահայտությունը։ Հավասարման աջ կողմի առաջին հատվածը՝ $\partial C / \partial a^L_j$-ը պարզապես ցույց է տալիս, թե ինչ արագությամբ է գնային ֆունկցիան փոփոխվում՝ կախված $j^{\rm րդ}$ ելքային ակտիվացիայից։ Օրինակ, եթե $C$-ն էապես կախված չէ տրված $j$ ելքային նեյրոնից, ապա $\delta^L_j$ կլինի բավականին փոքր՝ այն ինչ մենք սպասում էինք։ Աջակողմյան երկրորդ արտահայտությունը ցույց է տալիս $\sigma$ ակտիվացիայի ֆունկցիայի փոփոխման արագությունը՝ կախված $z^L_j$-ից։
Նկատենք, որ (BP1) արտահայտության բոլոր անդամները հեշտությամբ կարելի է հաշվել։ Հատկապես $z^L_j$-ը հաշվարկվում է ցանցի վարքագիծը հաշվելու ընթացքում և $\sigma'(z^L_j)$ հաշվարկումը պարզապես լրացուցիչ ոչ մեծ «գլխացավանք» է։ $\partial C / \partial a^L_j$ մասնական ածանցյալի տեսքն իհարկե կախված է գնային ֆունկցիայի տեսքից։ Սակայն, հաշվի առնելով, որ գնային ֆունկցիան հայտնի է, ապա $\partial C / \partial a^L_j$ հաշվարկումը նույնպես իրենից մեծ խնդիր չի ներկայացնում։ Օրինակ, եթե օգտագործում ենք քառակուսային գնային ֆունկցիան, ապա $C = \frac{1}{2} \sum_j (y_j-a^L_j)^2$, հետևաբար $\partial C / \partial a^L_j = (a_j^L-y_j)$ ինչը հեշտությամբ հաշվարկելի է։
(BP1) հավասարումը սահմանում է $\delta^L$ վեկտորի անդամները։ Հավասարումը չունի վեկտորական տեսք, ինչն անհրաժեշտ է հետադարձ տարածման համար, այնուամենայնիվ այն ճշգրիտ նկարագրում է ելքային շերտի սխալանքը։ Այսպիսով, $\delta^L$ արտահայտությունը կարելի է արտագրել մատրիցային տեսքով հետևյալ կերպ՝ \begin{eqnarray} \delta^L = \nabla_a C \odot \sigma'(z^L). \tag{BP1a}\end{eqnarray} Որտեղ $\nabla_a C$ սահմանվում է որպես վեկտոր, որի անդամներն են $\partial C / \partial a^L_j$ մասնական ածանցյալները։ $\nabla_a C$-ն կարելի է ընկալել որպես $C$ գնային ֆունկիայի փոփոխման գործակիցը՝ կախված ելքային ակտիվացիաներից։ Հեշտ է նկատել, որ (BP1a) և (BP1) հավասարումները համարժեք են։ Այդ պատճառով հաճախակի կօգտագործենք (BP1) հավասարումը։ Օրինակ, քառակուսային գնի ֆունկցիայի դեպքում $\nabla_a C = (a^L-y)$, հետևաբար (BP1) հավասարման մատրիցային տեսքը կլինի \begin{eqnarray} \delta^L = (a^L-y) \odot \sigma'(z^L). \tag{30}\end{eqnarray} Ինչպես տեսնում եք, այս հավասարումն ունի վեկտորական տեսք և այն կարելի է հեշտությամբ հաշվել՝ օգտագործելով Numpy գրադարանը։
$\delta^l$ սխալանաքի արտահայտումն ըստ հաջորդ շերտի $\delta^{l+1}$ սխալանքի։ Դիտարկենք հետևյալ հավասարումը. \begin{eqnarray} \delta^l = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^l), \tag{BP2}\end{eqnarray} որտեղ $(w^{l+1})^T$ կշիռների $w^{l+1}$ տրանսպոնացված մատրիցն է՝ $(l+1)^{\rm րդ}$ շերտի համար։ Այս հավասարումը կարող է բարդացված թվալ, սակայն յուրաքանչյուր անդամ ունի գեղեցիկ մեկնաբանություն։ Ենթադրենք, որ $(l+1)^{\rm րդ}$ շերտի $\delta^{l+1}$ սխալանքը հայտնի է։ $(w^{l+1})^T$ տրանսպոնացված կշիռների մատրիցի կիրառումը ինտուիտիվ կարելի է ընկալել որպես սխալանքը ցանցում հետադարձ շարժելու գործողություն, որը տալիս է $l^{\rm րդ}$ շերտի ելքային արժեքի սխալանքի որոշակի չափողականություն։ Այնուհետև կիրառում ենք $\odot \sigma'(z^l)$ Հադամարի արտադրյալը։ Այս գործողությամբ սխալանքը հետադարձ տեղափոխվում է $l$ շերտի ակտիվացիայի ֆունկցիային, որի արդյունքում ստանում ենք $\delta^l$ սխալանքը $l$ շերտի կշռված մուտքերի նկատմամբ։
Միավորելով (BP2) և (BP1) հավասարումները, կարող ենք $\delta^l$ սխալանքը հաշվել ցանցի կամայական շերտում։ Կսկսենք $\delta^L$-ի հաշվումից՝ օգտագործելով (BP1) հավասարումը, այնուհետև կօգտագործենք (BP2) հավասարումը, որպեսզի հաշվենք $\delta^{L-1}$ սխալանքը, այնուհետև կկրկնենք (BP2) հավասարման կիրառումը, որպեսզի հաշվենք $\delta^{L-2}$ և ատդպես շարունակ մինչև ցանցի «սկիզբը»
Գնային ֆունկցիայի փոփոխման գործակցի հավասարումը՝ կախված ցանցի շեղումներից։ Դիտարկենք հետևյալ հավասարումը. \begin{eqnarray} \frac{\partial C}{\partial b^l_j} = \delta^l_j. \tag{BP3}\end{eqnarray} Այն է, $\delta^l_j$ սխալանքը ճիշտ նույնն է, ինչ $\partial C / \partial b^l_j$ փոփոխման գործակիցը։ Սա հրաշալի նորություն է, քանի որ (BP1) և (BP2) արդեն ցույց են տվել, թե ինչպես կարելի է հաշվել $\delta^l_j$ սխալանքը։ Կարող ենք (BP3) հավասրումն արտագրել կարճ որպես \begin{eqnarray} \frac{\partial C}{\partial b} = \delta, \tag{31}\end{eqnarray} որտեք $\delta$ հաշվարկում ենք նույն նեյրոնի համար, ինչի համար դիտարկում էինք $b$ շեղումը։
Գնային ֆունկցիայի փոփոխման գործակցի հավասարումը՝ կախված ցանցի կշիռներից։ Դիտարկենք հետևյալ հավասարումը՝ \begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j. \tag{BP4}\end{eqnarray} Այն ցույց է տալիս, թե ինչպես կարելի է հաշվել $\partial C / \partial w^l_{jk}$ մասնական ածանցյալներն ըստ $\delta^l$ և $a^{l-1}$ մեծությունների, ինչը մենք արդեն գիտենք հաշվել։ Հավասարումը կարելի է արտահայտել ավելի կարճ տեսքով հետևյալ կերպ. \begin{eqnarray} \frac{\partial C}{\partial w} = a_{\rm in} \delta_{\rm out}, \tag{32}\end{eqnarray} որտեղ $a_{\rm in}$ մեծությունը $w$ կշիռների հետ միասին մուտք հանդիսացող նեյրոնի ակտիվացիան է և $\delta_{\rm out}$-ն նեյրոնի արդյունքի ելքային սխալանքն է $w$ կշիռների դեպքում։ Մոտիկից դիտելով $w$ կշռին և այն երկու նեյրոններին, որոնք կապակցված են այդ կշռով, կտեսնենք հետևյալ պատկերը
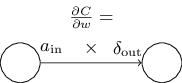
(BP1) - (BP4) . հավասարումներից կարելի է անել նաև այլ հետևություններ։ Դիտարկենք $\sigma'(z^L_j)$ արտահայտությունը (BP1) . հավասարման մեջ։ Հիշելով նախկին գլխում ներկայացված սիգմոիդ ֆունկցիայի գրաֆիկը որտեղ $\sigma$ ֆունկցիայի աճը շատ փոքրանում է երբ $\sigma(z^L_j)$ մոտենում է $0$ կամ $1$ արժեքներին։ Եվ այսպիսով, հետևությունն այն է, որ վերջին շերտի կշիռները դանդաղ կսովորեն, եթե ելքային նեյրոնն ունի թույլ ակտիվացիա ($\approx 0$) կամ ուժեղ ակտիվացիա ($\approx 1$)։ Այս դեպքում ասում են, որ ելքային նեյրոնը հագեցած (saturated) է և արդյունքում կշիռը դադարել է սովորել (կամ սովորում է շատ դանդաղ)։ Նմանատիպ պնդումներ կարելի է անել նաև ելքային նեյրոնի շեղումների մասին։
Նմանատիպ հետևություններ կարող ենք կատարել նաև միջանկյալ շերտերի դեպքում։ Դիտարկենք $\sigma'(z^l)$ արտահայտությունը (BP2) . հավասարման մեջ։ Պարզ է, որ $\delta^l_j$ ավելի հավանական է, որ փոքր լինի, եթե նեյրոնը մոտ է հագեցմանը։ Եվ սա, իր հերթին նշանակում է, որ յուրաքանչյուր կշիռների մուտք հագեցած նեյրոնին կսովորի դանդաղորեն* *Այս տրամաբանությունը տեղի չունի, երբ ${w^{l+1}}^T \delta^{l+1}$ արտահայտության արժեքն այնքան մեծ է, որը կոմպենսացնում է $\sigma'(z^l_j)$ փոքր լինելը։ Այստեղ խոսքը գնում է ընդհանուր տենդենցների մասին։ .
Այսպիսով, մենք սովորեցինք, որ կշիռը կսովորի դանդաղորեն, եթե մուտքային նեյրոնը թուլ ակտիվացիայով է կամ երբ ելքային նեյրոնը հագեցած է, այն է ունի ուժեղ կամ թույլ ակտիվացիա։
Այս դիտարկումներից ոչ մեկը չապազանց զարմանալի չէ։ Այնուամենայնիվ, դրանք նպաստում են, որպեսզի բարելավենք մեր մտավոր մոդելը այն մասին, թե ինչ է տեղի ունենում, երբ նեյրոնային ցանցը սովորում է։ Ավելին, մենք կարող ենք այս դիտարկումներն ընդհանրացնել։ Պարզվում է, որ չորս ֆունդամենտալ հավասարումները տեղի ունեն ոչ միայն կամայական ակտիվացիայի դեպքում, այլ ոչ միայն սիգմոիդ ֆունկցիայի (քիչ ուշ ապացույցներում կտեսնենք, որ $\sigma$ ֆունկիայի ոչ մի հատկություն չի օգտագործվում)։ Եվ այդպիսով, կարող ենք այդ հավասարումներն օգտագործել, որպեսզի նախագծենք այնպիսի ակտիվացիայի ֆունկցիաներ, որոնք ունեն որոշակի ցանկալի «ուսուցման հատկություններ»։ Օրինակ, պատկերացնելու համար, ենթադրենք, որ պետք է ընտրենք այնպիսի (ոչ սիգմոիդ) ակտիվացիայի ֆունկցիա $\sigma$, որ $\sigma'$ ածանցյալը միշտ դրական է և երբեք զրոյին չի մոտենում։ Դա կարող է խոչընդոտել ուսուցման դանդաղեցմանը, որը տեղի է ունենում, երբ սիգմոիդ նեյրոնները հագենում են։ Ավելի ուշ գրքում կտեսնենք օրինակներ, երբ այդպիսի փոփոխություններ են արվում ակտիվացիայի ֆունկցիային։ Մտապահելով (BP1) - (BP4) հավասարումները, կօգնի բացատրել, թե ինչու են նմանատիպ փոփոխությունները փորձարկվում և ինչ ազդեցություն կարող են ունենալ։

Խինդիր
- Հետադարձ տարածման հավասարումների այլընտրանքային ներկայացում. Հետադարձ տարածման հավասարումները (ավելի հստակ (BP1) և (BP2) հավասարումները) սկսեցինք օգտագործելով Հադամարի արտադրյալը։ Եթե ծանոթ չեք Հադամարի արտադրյալին, ապա այդ ներկայացումը կարող է շփոթեցնել։ Գոյություն ունի այլընտրանքային մոտեցում՝ հիմնված մատրիցների բազմապատկման վրա, որը որոշ ընթերցողներ կարող են բավականին ուսուցողական համարել։ (1) Ցույց տվեք, որ (BP1) հավասարումը կարող ենք արտահայտել հետևյալ կերպ՝ \begin{eqnarray} \delta^L = \Sigma'(z^L) \nabla_a C, \tag{33}\end{eqnarray} որտեղ $\Sigma'(z^L)$ քառակուսային մատրից է, որի անկյունագծային տարրերն ունեն $\sigma'(z^L_j)$ արժեքները և մնացած անդամներն ունեն զրոյական արժեք։ Նկատտենք, որ այդ մատրիցը կիրառվում է $\nabla_a C$-ի վրա որպես մատրիցային բազմապատկում։ (2) Ցույց տվեք, որ (BP2) կարելի է ներկայացնել որպես \begin{eqnarray} \delta^l = \Sigma'(z^l) (w^{l+1})^T \delta^{l+1}. \tag{34}\end{eqnarray} (3) Միավորելով (1) և (2) խնդիրները, ցույց տվեք, որ \begin{eqnarray} \delta^l = \Sigma'(z^l) (w^{l+1})^T \ldots \Sigma'(z^{L-1}) (w^L)^T \Sigma'(z^L) \nabla_a C \tag{35}\end{eqnarray} Այն ընթերցողները, որոնք հարմարավետ են իրենց զգում մատրիցային բազմապատկումների հետ, ապա այս հավասարումն ավելի հեշտ ընկալեն, քան (BP1) և (BP2) հավասարումները։ (BP1) և (BP2) հավասարումների վրա կենտրոնանալու նպատակն այն է, որ այդ մոտեցման իրականացումն ավելի արագ է թվային առումով։
Չորս հիմնական հավասարումների ապացույցները (ընտրովի)
Ապացուցենք չորս հիմնական հավասարումները՝ (BP1) - (BP4) ։ Չորս հավասարումներն էլ հետևում են շատ փոփոխականի հաշվում բարդ ֆունկցիայի ածանցյալի կանոնից։ Եթե լավ եք տիրապետում բարդ ֆունկցիայի ածանցյալի կանոնին, ապա խորհուրդ եմ տալիս փորձել ինքնուրույն դուրս բերել մինչ դուրս բերումները կարդալը։
Սկսենք (BP1) հավասարումով, որը ցույց է տալիս ելքի $\delta^L$ սխալանքը։ Հիշենք, որ ըստ սահմանման \begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial z^L_j}. \tag{36}\end{eqnarray} Կիրառելով բարդ ֆունկցիայի ածանցման կանոնը, կարող ենք վերևի մասնական ածանցյալը վերարտահայտել ելքային ակտիվացիաներից կախված մասնական ածանցյալների միջոցով \begin{eqnarray} \delta^L_j = \sum_k \frac{\partial C}{\partial a^L_k} \frac{\partial a^L_k}{\partial z^L_j}, \tag{37}\end{eqnarray} որտեղ գումարն ըստ ելքային շեւրտի $k$ նեյրոնների է։ Իհարկե, $k^{\rm րդ}$ նեյրոնի $a^L_k$ ակտիվացիան կախված է $j^{\rm րդ}$ նեյրոնի $z^L_j$ կշռված մուտքից միայն այն դեպքում, երբ $k = j$։ Եվ այսպիսով, $\partial a^L_k / \partial z^L_j$ վերանում է, երբ $k \neq j$։ Այսպիսով հավասարումն կարելի է պարզեցնել. \begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \frac{\partial a^L_j}{\partial z^L_j}. \tag{38}\end{eqnarray} Նկատենք, որ $a^L_j = \sigma(z^L_j)$, ապա աջ կողմում գտնվող երկրորդ արտահայտությունը կարելի է արտահայտել որպես $\sigma'(z^L_j)$ և հավասարումը կվերածվի հետևյալ տեսքի \begin{eqnarray} \delta^L_j = \frac{\partial C}{\partial a^L_j} \sigma'(z^L_j), \tag{39}\end{eqnarray} որը պարզապես (BP1) հավասարումն է՝ արտահայտված անդամների միջոցով։
Հաջորդիվ, կապացուցենք (BP2) հավասարումը, որը $\delta^l$ սխալանքն արտահայտում է ըստ հաջորդ շերտի $\delta^{l+1}$ սխալանքի։ Այդ նպատակով, փորձենք $\delta^l_j = \partial C / \partial z^l_j$ արտահայտենք ըստ $\delta^{l+1}_k = \partial C / \partial z^{l+1}_k$, օգտագործելով բարդ ֆունկցիայի դիֆերենցման կանոնը։ \begin{eqnarray} \delta^l_j & = & \frac{\partial C}{\partial z^l_j} \tag{40}\\ & = & \sum_k \frac{\partial C}{\partial z^{l+1}_k} \frac{\partial z^{l+1}_k}{\partial z^l_j} \tag{41}\\ & = & \sum_k \frac{\partial z^{l+1}_k}{\partial z^l_j} \delta^{l+1}_k, \tag{42}\end{eqnarray} որտեղ վերջին տողում մենք երկու արտահայտությունները շրջել ենք տեղերով և աջ կողմը փոխարինել $\delta^{l+1}_k$ արտահայտությամբ ըստ սահմանման։ Վերջին տողի առաջին անդամը հաշվելու համար, հաշվի առնենք, որ \begin{eqnarray} z^{l+1}_k = \sum_j w^{l+1}_{kj} a^l_j +b^{l+1}_k = \sum_j w^{l+1}_{kj} \sigma(z^l_j) +b^{l+1}_k. \tag{43}\end{eqnarray} Դիֆերենցելով կստանանք հետևյալ արտահայտությունը՝ \begin{eqnarray} \frac{\partial z^{l+1}_k}{\partial z^l_j} = w^{l+1}_{kj} \sigma'(z^l_j). \tag{44}\end{eqnarray} Տեղադրելով ստացվածը (42) հավասարման մեջ, կստանանք \begin{eqnarray} \delta^l_j = \sum_k w^{l+1}_{kj} \delta^{l+1}_k \sigma'(z^l_j). \tag{45}\end{eqnarray} Սա պարզապես (BP2) հավասարումն է գրված էլեմենտ առ էլեմենտ տեսքով։
Վերջին երկու հավասարումները, որ կապացուցենք, դրանք (BP3) և (BP4) հավասարումներն են, որոնք նույնպես հետևում են բարդ ֆունկցիայի դիֆերենցիալի կանոնից՝ շատ նման վերևում բերված ապացույցներին։ Դա թողնում են ընթերցողին որպես վարժություն.
Վարժություն
- Ապացուցել (BP3) և (BP4) հավասարումները։
Այսքանով ավարտում ենք հետադարձ տարածման հիմնական հավասարումների ապացույցը։ Ապացույցը կարող է դժվար թվալ։ Սակայն այն պարզապես բարդ ֆունկցիաների դիֆերենցման կանոնի հմտորեն կիրառման հետևանք է։ Այլ կերպ ասած, կարող ենք պատկերացնել, որ հետադարձ տարածումը դա գնային ֆունկցիայի գրադիենտի հաշվման եղանակ է, որը հիմնված է շատ փոփոխականի բարդ ֆունկցիաների դիֆերենցման կանոնի սիստեմատիկ օգտագործման վրա։ Դա, ըստ էության նկարագրում է հետադարձ տարածման հիմնական գաղափարը, իսկ մնացածն ուղղակի մանրամասներ են։
Հետադարձ տարածման ալգորիթմը
Հետադարձ տարածման հավասարումները ցույց են տալիս, թե ինչպես կարելի է հաշվել գնային ֆունկցիայի գրադիենտը։ Արտահայտենք դա ալգորիթմի տեսքով.
-
Մուտք $x$: $a^{1}$ ակտիվացիայի շերտը սկզբնավորենք մուտքային շերտով։
-
Առաջաբերում (Feedforward): Յուրաքանչյուր $l = 2, 3, \ldots, L$ շերտերի համար հաշվել $z^{l} = w^l a^{l-1}+b^l$ and $a^{l} = \sigma(z^{l})$.
-
Ելքային սխալանք $\delta^L$: Հաշվել $\delta^{L} = \nabla_a C \odot \sigma'(z^L)$ վեկտորը։
-
Սխալանքի հետադարձ տարածումը (Backpropagate)։ Յուրաքանչյուր $l = L-1, L-2, \ldots, 2$ շերտի համար հաշվել $\delta^{l} = ((w^{l+1})^T \delta^{l+1}) \odot \sigma'(z^{l})$.
- Ելք: Գնային ֆունկցիայի գրադիենտը տրվում է $\frac{\partial C}{\partial w^l_{jk}} = a^{l-1}_k \delta^l_j$ և $\frac{\partial C}{\partial b^l_j} = \delta^l_j$ հավասարումներով։
Դիտարկելով ալգորիթմը, կարելի է տեսնել, թե ինչու է այն կոչվում հատադարձ տարածում։ Սխալանքի վեկտորները հետադարձ հաշվարկվում են՝ սկսելով վերջին շերտից։ Հետադարձ գործողությունը հետվանք է այն բանի, որ գնային ֆունկցիան կախված է ցանցի ելքային արժեքներից։ Որպեսզի հասկանանք գնի փոփոխությունը կախված կշիռներից և շեղումներից, պետք է կրկնողաբար կիրառենք բարդ ֆունկցիայի դիֆերենցման կանոնը, հետ վերադառնալով շերտ առ շերտ, որպեսզի ստանանք համապատասխան արտահայտությունները։
Վարժություններ
-
Հետադարձ տարածում միակ փոփոխության ենտարկված նեյրոնով։
Ենթադրենք, որ տրված է առաջաբեր նեյրոնային ցանց, որտեղ գոյություն ունի միայն մեկ նեյրոն, որը փոփոխության է ենտարկված, այնպես, որ նեյրոնի ելքային արժեքը տրված է $f(\sum_j w_j x_j + b)$ արտահայտությամբ, որտեղ $f$ որևէ ֆունկցիա
է բացի սիգմոիդից։ Ինչպես պետք է փոփոխության ենթարկենք հետադարձ տարածման ալգորիթմն այս դեպքում։
- Գծային նեյրոններով հետադարձ տարածում։ Ենթադրենք, որ $\sigma$ ոչ գծային ֆունկցիան փոխարինել ենք $\sigma(z) = z$ գծային ֆուննկցիայով ամբողջ ցանցի համար։ Վերաձևակերպեք հետադարձ տարածման ալգորիմթմն այս դեպքում։
Ինչպես վերևում նկարագրված է, հետադարձ տարածման ալգորիթմը հաշվում է գնային ֆունկցիայի գրադիենտը տրված $C = C_x$ մարզման օրինակի համար։ Հաճախ հետադարձ տարածումը միավորվում է այնպիսի ուսուցման ալգորիթմի հետ, ինչպիսին է ստոկաստիկ գրադիենտային վայրէջքը, որտեղ գրադիենտը հաշվարկվում է բազմաթիվ օրինակների հիման վրա։ Տրված $m$ մարզման օրինակների մինի-փաթեթի համար, հետևյալ ալգորիթմը կիրառում է գրադիենտային վայրէջքի ուսուցման քայլը՝ հիմնված այդ մինի-փաթեթի վրա։
-
Մուտքագրեք մարզման օրինակների բազմությունը։
-
Յուրաքանչյուր $x$ մարզման օրինակի համար. Սկզբնավորենք համապատասխան $a^{x,1}$ մուտքային ակտիվացիան և կատարենք հետևյալ քայլերը.
-
Առաջաբերում (Feedforward): Յուրաքանչյուր $l = 2, 3, \ldots, L$ շերտի համար հաշվենք $z^{x,l} = w^l a^{x,l-1}+b^l$ և $a^{x,l} = \sigma(z^{x,l})$ արտահայտությունների արժեքները։
-
Ելքային սխալանքը՝ $\delta^{x,L}$: Վեկտորի հաշվումը. $\delta^{x,L} = \nabla_a C_x \odot \sigma'(z^{x,L})$.
- Սխալանքի հետադարձ տարածումը: Յուրաքանչյուր $l = L-1, L-2, \ldots, 2$ հաշվել $\delta^{x,l} = ((w^{l+1})^T \delta^{x,l+1}) \odot \sigma'(z^{x,l})$.
-
Առաջաբերում (Feedforward): Յուրաքանչյուր $l = 2, 3, \ldots, L$ շերտի համար հաշվենք $z^{x,l} = w^l a^{x,l-1}+b^l$ և $a^{x,l} = \sigma(z^{x,l})$ արտահայտությունների արժեքները։
-
Գրադիենտային վայրէջք: Յուրաքանչյուր $l = L, L-1, \ldots, 2$ թարմացնել կշիռները ըստ հետևյալ կանոնի՝ $w^l \rightarrow w^l-\frac{\eta}{m} \sum_x \delta^{x,l} (a^{x,l-1})^T$, և շեղումներն ըստ $b^l \rightarrow b^l-\frac{\eta}{m}
\sum_x \delta^{x,l}$ կանոնի.
Հետադարձ տարածման իրականացման կոդը
Ըմբռնելով հետադարձ տարածման աբստրակտ տարբերակը կարելի է առաջ անցնել և դիտարկել նախկին գլխում օգտագործված հետադարձ տարածման իրականացման կոդը։ Հիշենք նախորդ գլխից, որ կոդը զետեղված է Network դասի update_mini_batch և backprop մեթոդներում։ Այս մեթոդների կոդը վերևում նկարագրված ալգորիթմների ուղիղ թարգմանությունն է։ Մասնավորապես update_mini_batch մեթոդը թարմացնում է Network-ի կշիռներն ու շեղումները՝ հաշվելով ընթացիկ մարզման օրինակների mini_batch-ի գրադիենտը.
class Network(object):
...
def update_mini_batch(self, mini_batch, eta):
"""Update the network's weights and biases by applying
gradient descent using backpropagation to a single mini batch.
The "mini_batch" is a list of tuples "(x, y)", and "eta"
is the learning rate."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]
class Network(object):
...
def backprop(self, x, y):
"""Return a tuple "(nabla_b, nabla_w)" representing the
gradient for the cost function C_x. "nabla_b" and
"nabla_w" are layer-by-layer lists of numpy arrays, similar
to "self.biases" and "self.weights"."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# feedforward
activation = x
activations = [x] # list to store all the activations, layer by layer
zs = [] # list to store all the z vectors, layer by layer
for b, w in zip(self.biases, self.weights):
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid(z)
activations.append(activation)
# backward pass
delta = self.cost_derivative(activations[-1], y) * \
sigmoid_prime(zs[-1])
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
# Note that the variable l in the loop below is used a little
# differently to the notation in Chapter 2 of the book. Here,
# l = 1 means the last layer of neurons, l = 2 is the
# second-last layer, and so on. It's a renumbering of the
# scheme in the book, used here to take advantage of the fact
# that Python can use negative indices in lists.
for l in xrange(2, self.num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
return (nabla_b, nabla_w)
...
def cost_derivative(self, output_activations, y):
"""Return the vector of partial derivatives \partial C_x /
\partial a for the output activations."""
return (output_activations-y)
def sigmoid(z):
"""The sigmoid function."""
return 1.0/(1.0+np.exp(-z))
def sigmoid_prime(z):
"""Derivative of the sigmoid function."""
return sigmoid(z)*(1-sigmoid(z))
Խնդիր
- Լրիվ մատրիցային մոտեցում մինի-փաթեթով հետադարձ տարածման համար։ Մեր ստոկաստիկ գրադիենտային վայրէջքը անցնում է մարզման օրինակների վրայով մինի-փաթեթում։ Հնարավոր է կատարել այնպիսի փոփոխություն, որի արդյունքում հետադարձ տարածման ալգորիթմը միաժամանակ կհաշվի բոլոր օրինակների գրադիենտները մինի-փաթեթում։ Գաղափարը կայանում է նրանում, որ մեկ $x$ մուտքային վեկտորից սկսելու փոխարեն, կարող ենք սկսել $X = [x_1 x_2 \ldots x_m]$ մատրիցով, որի սյունակները մինի-փաթեթի վեկտորներն են։ Առաջ տարածումը (forward-propagate) կատարվում է կշիռների մատրիցով բազմապատկման, շեղումների մատրիցով գումարման և սիգմոիդ ֆունկցիայի կիրառմամբ մատրիցի բոլոր էլեմենտներին։ Հետադարձ տարածումը կատարվում է նմանատիպ մոտեցումներով։ Կառուցեք հետադարձ տարածման պսեվդոկոդը համաձայն այս մոտեցման։ Փոփոխեք network.py այնպես, որ այն օգտագործի մատրիցային մոտեցումը։ Այս մոտեցման առավելությունը կայանում է նրանում, որ այն օգտագործում է ժամանակակից գծային հանրահաշվի գրադարանների լայն հնարավորությունները։ Արդյունքում այն էապես ավելի արագ կլինի, քան մինի-փաթեթի վրա կառուցված ցիկլը։ (Իմ լափթոփի վրա, օրինակ, մոտ երկու անգամ ավելի արագ է, երբ գործարկում եմ MNIST դասակարգման խնդիրների վրա, նկարագրված նախորդ գլխում։) Պրակտիկորեն բոլոր լուրջ գրադարանները, որոնք իրականացնում են հետադարձ տարածում, օգտագործում այս են մատրիցային մոտեցման ինչ-որ տարբերակ։
Ի՞նչ իմաստով է հետադարձ տարածումն արագագործ ալգորիթմ
Ի՞նչ իմաստով է հետադարձ տարածումն արագագործ ալգորիթմ։ Այս հարցին պատասխանելու համար դիտարկենք գրադիենտի հաշվման այլ մոտեցում։ Պատկերացրեք նեյրոնային ցանցերի հետազոտությունների սկզբնական շրջանում ենք՝ 1950-ականներ կամ 1960-ականներ։ Դուք առաջին մարդն եք աշխարհում, որ մտածում է գրադիենտային վայրէջքն օգտագործել ուսուցման համար։ Սակայն որպեսզի ալգորիթմն աշխատի, անհրաժեշտ է մի եղանակ, որով կարելի է հաշվել գնային ֆունկցիայի գրադիենտը։ Հետ նայելով ձեր մաթեմատիկական անալիզի գիտելիքներին, փորձում եք տեսնել արդյոք բարդ ֆունկցիայի դիֆերենցման կանոնով կարելի է փորձել լուծել այս խնդիրը։ Սակայն որոշ ժամանակ փորձելուց հետո գաղափարը բարդ է թվում և դուք հուսահատվում եք։ Հետևաբար փորձում եք այլ մոտեցում փնտրել և դիտարկել գնի ֆունկցիան կախված միայն կշիռներից $C = C(w)$ (շեղումներին դեռ կվերադառնանք)։ Այնուհետև համարակալում եք կշիռները՝ $w_1, w_2, \ldots$ և հաշվում $\partial C / \partial w_j$ մասնական ածանցյալները տրված $w_j$ կշռի համար։ Կարելի է օգտագործել հետևյալ մոտարկումը՝ \begin{eqnarray} \frac{\partial C}{\partial w_{j}} \approx \frac{C(w+\epsilon e_j)-C(w)}{\epsilon}, \tag{46}\end{eqnarray} որտեղ $\epsilon > 0$ փոքր դրական թիվ է և $e_j$ միավոր վեկտորն է $j^{\rm րդ}$ ուղղության վրա։ Այսպիսով, կարող ենք գնահատել $\partial C / \partial w_j$ մասնական ածանցյալները հաշվելով $C$ գինը երկու տարբեր (իրար մոտ) $w_j$ արժեքների համար և կիրառել (46) հավասարումը։ Նույն ձևով կարող ենք հաշվել նաև $\partial C / \partial b$ շեղումների դեպքում։
Այս մոտեցումը խոստումնալից է թվում։ Այն հիմնված է համեմատաբար պարզ կոնցեպտների վրա և բավականին դյուրին է իրականացնելը՝ օգտագործելով մի քանի տող կոդ։ Իրոք, այն ավելի խոստումնալից է թվում քան բարդ ֆունկցիայի ածանցյալն օգտագործելով գրադիենտ հաշվելը։
Դժբախտաբար, մինչդեռ այս մոտեցումը խոստումնալից է թվում, իրականացումը բավականին դանդաղագործ է։ Որպեսզի հասկանանք պատճառները, ենթադրենք, որ մեր ցանցում ունենք միլիոն կշիռներ։ Յուրաքանչյուր տարբեր $w_j$ կշռի համար հաշվենք $C(w+\epsilon e_j)$, որպեսզի հաշվենք $\partial C / \partial w_j$ մասնական ածանցյալը։ Այսեղից հետևում է, որպեսզի հաշվենք գրադիենտը, պետք է գնային ֆունկցիայի արժեքը միլիոն անգամներ հաշվենք, ինչի հետևանքով միլիոն անգամ պետք է առաջ շարժվենք ցանցով։ Դա չի ներառում $C(w)$ արժեքի հաշվումը։
Հետադարձ տարածման գեղեցկությունը կայանում է նրանում, որ այն միաժամանակ հաշվում է բոլոր $\partial C / \partial w_j$ մասնական ածանցյալները՝ օգտագործելով միայն մեկ առաջ տարածում և մեկ հետադարձ տարածում ցանցով։ Հետադարձ առաջխաղացման հաշվարկային արագությունը (computational cost) համարյա նույնն է, ինչ առաջ տարածման* *Դա հնարավոր է, սակայն ճշգրիտ արտահայտությունն անելու համար որոշակի անալիզ և հետազոտություն է հարկավոր։ Ինչու՞ է հնարավոր, քանզի առաջ տարածման դեպքում հաշվարկային գինը հիմնականում բաղկացած է կշիռների մատրիցով բազմապատկումներից, իսկ հետադարձ տարածման դեպքում տրանսպոնացված կշիռների մատրիցներով բազմապատկումից։ Հետևաբար այդ գործողություններն ունեն նմանատիպ հաշվարկային բարդություններ։ ։ Հետևաբար հետադարձ տարածման ընդհանուր հաշվարկաւյին գինը նույնն է, ինչ ցանցում երկու առաջաբեր գործողություն կատարելիս։ Համեմատեք դա միլիոնից ավել առաջաբեր գործողությունների հետ, որ անհրաժեշտ կլիներ, եթե մենք որդեգրեինք ներքևում նշված հավասարման հիման վրա կառուցված մեթոդը։ (46) Եվ այսպիսով, չնայած նրան, որ հետադարձ տարածումն ունի բավականին բարդ տեսք, քան (46) մոտեցումը, այն անհամեմատ ավելի արագագործ է։
Այս «արագացումն» առաջին անգամ գնահատվել է 1986 թվականին և այն էապես ընդլայնել է խնդիրների ցանկը, որոնք կարելի է լուծել նեյրոնային ցանցերի միջոցով։ Արդյունքում, այն ստեղծեց մարդկանց ներհոսք դեպի նեյրոնային ցանցեր։ Իհարկե, հետադարձ տարածումը «դարման չէ բոլոր վերքերի»։ Անգամ 1980-ականների վերջերին սահմանափակումներ ծառացան գիտնականների առջև, հատկապես երբ այն փորձվեց օգտագործել խորը ցանցերի ուսուցման մեջ (բազմաթիվ շերտերով ցանցերի)։ Հետագայում կտեսնենք, թե ինչպես ժամանակակից համակարգիչները և որոշ խելացի գաղափարներ հնարավոր են դարձնում հետադարձ տարածման օգտագործումը այդպիսի ցանցերի մարզման համար։
Հետադարձ տարածում. ամբողջական պատկերը
Այսպիսով, գոյություն ունեն երկու առեղծվածներ կապված հետադարձ տարածման հետ։ Առաջին. ի՞նչ է ըստ էության ալգորիթմն անում։ Իհարկե, մենք ցույց տվեցինք, որ սխալանքը ելքից տարածվում է դեպի ետ, սակայն արդյո՞ք կարող ենք ավելի խորանալ և ձեռք բերել ինտուցիա այն մասին, թե ինչ է տեղի ունենում երբ մենք այսքան մատրիցներ և վեկտորներ իրար ենք բազմապատկում։ Երկրոդ առեղծխվածն այն է, թե ինչպե՞ս կարելի է հայտնագործել հետադարձ տարածման ալգորիթմը։ Իհարկե կարելի է հետևել և հասկանալ ալգորիթմի քայլերն ու ապացույցը, սակայն արդյո՞ք խնդիրը հասկանում ենք այնքան խորությամբ, որ կարող էինք ալգրորիթմն ինքնուրույն հայտնագործել։ Արդյոք կա տրամաբանական շղթա, որին հետևելով կարող էինք հանգել հետադարձ տարածման ալգորիթմին։ Այս հատվածում կդիտարկենք այդ երկու առեղծվածները։
Որպեսզի մեր ինտուցիան այս ալգորիթմի վերաբերյալ բարելավենք, ենթադերնք, որ ցանցի որևիցե $w^l_{jk}$ կշռի նկատմամբ կիրառել ենք $\Delta w^l_{jk}$ փոփոխությունը.
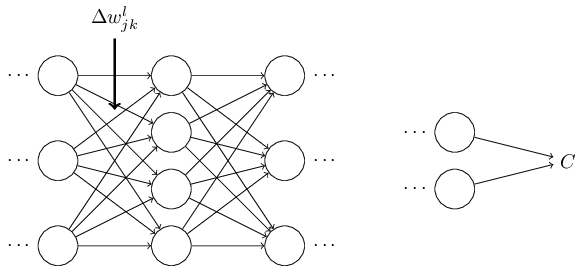
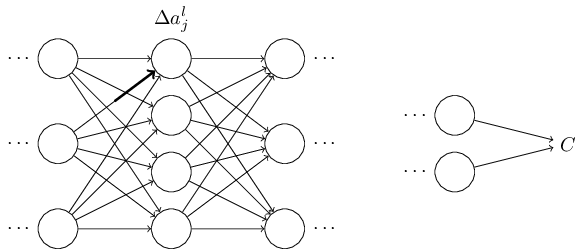
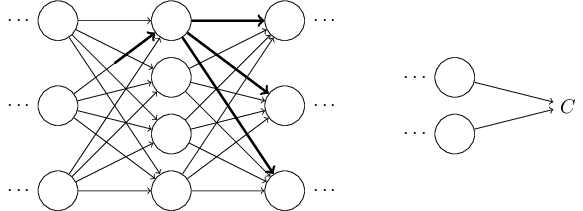
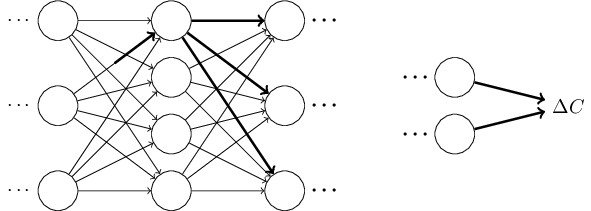
Փորձենք դա իրականացնել։ $\Delta w^l_{jk}$ փոփոխությունն առաջացնում է $\Delta a^{l}_j$ փոքրիկ փոփոխությունը $l^{\rm րդ}$ շերտի $j^{\rm րդ}$ ակտիվացիայում։ Այդ փոփոխությունը կարելի է նկարագրել հետևյալ կերպ։ \begin{eqnarray} \Delta a^l_j \approx \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk}. \tag{48}\end{eqnarray} Փոփոխությունը $\Delta a^l_{j}$ ակտիվացիայում կառաջացնի փոփոխություններ հաջորդ բոլոր շերտերի ակտիվացիաներում, օրինակ, $(l+1)^{\rm րդ}$ շերտում։ Դիտարկենք, թե ինչպես է փոփոխվում այդ ակտիվացիաներից որևիցէ մեկը, օրինակ՝ $a^{l+1}_q$։
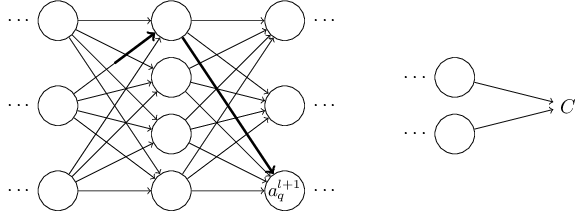
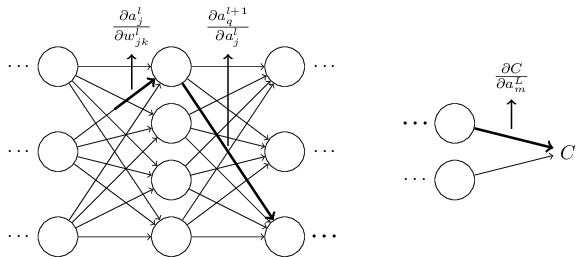
What I've been providing up to now is a heuristic argument, a way of thinking about what's going on when you perturb a weight in a network. Let me sketch out a line of thinking you could use to further develop this argument. First, you could derive explicit expressions for all the individual partial derivatives in Equation (53) . That's easy to do with a bit of calculus. Having done that, you could then try to figure out how to write all the sums over indices as matrix multiplications. This turns out to be tedious, and requires some persistence, but not extraordinary insight. After doing all this, and then simplifying as much as possible, what you discover is that you end up with exactly the backpropagation algorithm! And so you can think of the backpropagation algorithm as providing a way of computing the sum over the rate factor for all these paths. Or, to put it slightly differently, the backpropagation algorithm is a clever way of keeping track of small perturbations to the weights (and biases) as they propagate through the network, reach the output, and then affect the cost.
Now, I'm not going to work through all this here. It's messy and requires considerable care to work through all the details. If you're up for a challenge, you may enjoy attempting it. And even if not, I hope this line of thinking gives you some insight into what backpropagation is accomplishing.
What about the other mystery - how backpropagation could have been discovered in the first place? In fact, if you follow the approach I just sketched you will discover a proof of backpropagation. Unfortunately, the proof is quite a bit longer and more complicated than the one I described earlier in this chapter. So how was that short (but more mysterious) proof discovered? What you find when you write out all the details of the long proof is that, after the fact, there are several obvious simplifications staring you in the face. You make those simplifications, get a shorter proof, and write that out. And then several more obvious simplifications jump out at you. So you repeat again. The result after a few iterations is the proof we saw earlier* *There is one clever step required. In Equation (53) the intermediate variables are activations like $a_q^{l+1}$. The clever idea is to switch to using weighted inputs, like $z^{l+1}_q$, as the intermediate variables. If you don't have this idea, and instead continue using the activations $a^{l+1}_q$, the proof you obtain turns out to be slightly more complex than the proof given earlier in the chapter. - short, but somewhat obscure, because all the signposts to its construction have been removed! I am, of course, asking you to trust me on this, but there really is no great mystery to the origin of the earlier proof. It's just a lot of hard work simplifying the proof I've sketched in this section.
