Նեյրոնային ցանցեր և խորը ուսուցում
Խնդիրների և վարժությունների մասին
 Ձեռագիր թվանշանների ճանաչում՝ օգտագործելով նեյրոնային ցանցեր
Ձեռագիր թվանշանների ճանաչում՝ օգտագործելով նեյրոնային ցանցեր
 Ինչպե՞ս է աշխատում հետադարձ տարածումը
Ինչպե՞ս է աշխատում հետադարձ տարածումը
 Նեյրոնային ցանցերի ուսուցման բարելավումը
Նեյրոնային ցանցերի ուսուցման բարելավումը
 Տեսողական ապացույց այն մասին, որ նեյրոնային ֆունկցիաները կարող են մոտարկել կամայական ֆունկցիա
Տեսողական ապացույց այն մասին, որ նեյրոնային ֆունկցիաները կարող են մոտարկել կամայական ֆունկցիա
 Ինչու՞մն է կայանում նեյրոնային ցանցերի մարզման բարդությունը
Ինչու՞մն է կայանում նեյրոնային ցանցերի մարզման բարդությունը
Հավելված: Արդյո՞ք գոյություն ունի ինտելեկտի պարզ ալգորիթմ





Մարդկային տեսողական համակարգը աշխարհի հրաշալիքներից է: Դիտարկենք ձեռագիր թվանշանների հետևյալ հերթականությունը:
Մարդկանց մեծամասնությունը առանց ջանք գործադրելու կարող է ճանաչել 504192 թվերը: Այդ դյուրինությունը խաբուսիկ է սակայն: Մարդկային ուղեղի կիսագնդերում պարունակվում է հիմնական տեսողական կորտեքսը, որը հայտնի է որպես V1: Այն պարունակում է 140 միլիոն նեյրոններ, որոնք իրար հետ կապված են տասնյակ միլիարդավոր կապերով: Ընդ որում, մարդկային տեսողությունը բաղկացած չէ միայն V1-ից, այլ V2, V3, V4, և V5 տեսողական կորտեքսներից, որոնք իրականացնում են բազմաթիվ նկարների մշակում: Մեր գլուխներն ըստ էության պարունակում են սուպեր համակարգիչներ` էվոլյուցիայի միջոցով կատարելագործված միլիոնավոր տարիների ընթացքում և հրաշալիորեն հարմարված տեսանելի աշխարհը հասկանալու համար: Ձեռագիր թվանշանները հասկանալը հեշտ չէ, այնուամենայնիվ, մարկանց մոտ լավ է ստացվում հասկանալ այն ինչ իրենց աչքերն են ընկալում: Սակայն գրեթե ամբողջ այդ աշխատանքը կատարվում է ենթագիտակցորեն, հետևաբար մենք ըստ արժանվույն չենք գնահատում թե ինչպիսի դժվար խնդիր է լուծում տեսողական համակարգը:
Տեսողական համակարգի օրինաչափությունը հասկանալու դժվարությունը երևան է գալիս այն ժամանակ, երբ փորձ է արվում ստեղծել ծրագիր ձեռագիր թվանշաններ ճանաչելու համար: Մեզ հեշտ թվացող այդ երևույթը պարզվում է, որ բավականին բարդ է: Պատկերներ ճանաչելու պարզ ինտուիցիան (օրինակ, 9 թվանշանը վերևում շրջանաձև է, որը կապվում է նրեքևի հետ կոր ուղղաձիգով) պարզվում է որ այնքան էլ պարզ չէ, թե ինչպես նկարագրել ալգորիթմորեն: Երբ փորձ է կատարվում նպանատիպ կանոնները հստակեցնելու, անմիջապես խճճվում ենք բացառությունների կամ հատուկ դեպքերի կծիկի մեջ: Արագորեն հուսալքվում ենք խնդրի լուծման հարցում:
Նեյրոնային ցանցերը խնդրին մոտենում են այլ կերպ: Միտքը կայանում է նրանում, որ պետք է վերցնել մեծ քանակությամբ ձեռագիր թվանշաններ, որոնց կանվանենք մարզման օրինակներ,

և կառուցել այնպիսի համակարգ, որը կարող է սովորել այդ օրինակներից: Այլ կերպ ասած, նեյրոնային ցանցը օգտագործում է օրինակները ձեռագիր թվանշանների կառուցվածքն ինքնաբերաբար հասկանալու համար: Ավելին, շատացնելով օրինակների քանակը, ցանցը կարող է ավելի շատ ուսուցանել ձեռագրերի մասին, այսպիսով բարելավելով գուշակման ճշգրտությունը: Օրինակ, ցանցը ավելի ճշգրիտ կարող է գուշակել սովորելով 1000 օրինակի վրա քան 100 օրինակի:
Այս գլխում կկառուցենք համակարգչային ծրագիր, որը իրականացնում է նեյրոնային ցանց, որն իր հերթին սովորում է ճանաչել ձեռագիր թվանշանները: Ծրագիրը ունի 74 տող երկարություն և չի օգտագործում ոչ մի նեյրոնային ցանցերի գրադարան: Սակայն այն կարող է թվանշանները ճանաչել 96 տոկոս ճշտությամբ առանց մարդկային միջամտության: Այնուհետև հետագա գլուխներում կկառուցենք գաղափարներ, որոնք կօգնեն ճանաչման ճշտությունը հասցնել 99 տոկոսից ավելիին: Փաստացիորեն, լավագույն կոմերցիոն նեյրոնային ցանցերն այնքան հուսալի են, որ օգտագործվում են բանկերի կողմից չեկերի մշակման համար, փոստատների կողմից հասցեների ճանաչման համար:
Մենք կենտրոնանում ենք ձեռագիր թվանշանների ճանաչման վրա, քանի որ այն նեյրոնային ցանցերի մասին սովորելու համար գերազանց նախատիպային խնդիր է: Որպես նախատիպային խնդիր ըստ երևույթին այն հեշտ չէ, սակայն այնքան բարդ չէ որ կարիք զգացվի չափազանց բարդ լուծման տեխնիկաների կամ համակարգչային հզորության (computational power) օգտագործման: Հետևաբար սա հրաշալի մոտեցում է ավելի առաջադեմ տեխնիկաների հմտություններ յուրացնելու հարցում, օրինակ խորը ուսուցումը: Այսպիսով, գրքում պարբերաբար վերադառնալու ենք ձեռագիր թվանշանների ճանաչման խնդրին: Ավելի ուշ նաև կքննարկենք թե ինչպես կարելի է օգտագործել այս գաղափարները այլ խնդիրների լուծման համար, օրինակ` համակարգչային տեսողության (computer vision), բնական լեզվի ճանաչում (speech, natural language processing) և այլն:
Իհարկե, եթե այս գլխի նպատակը լիներ միայն ձեռագիր թվանշաններ ճանաչող ծրագրի կառուցումը, ապա գլուխն ավելի քիչ ծավալուն կլիներ: Մենք խոսելու ենք նաև նեյրոնային ցանցերի մասին այլ կարևոր գաղափարներից, հատկապես երկու կարևոր արհեստական նեյրոնների տեսակների մասին՝ պերսեպտրոն և սիգմոիդ նեյրոն, ինչպես նաև նեյրոնային ցանցերի ստանդարտ ուսուցման ալգորիթմի մասին, որը հայտնի է որպես ստոկաստիկ գրադիենտային վայէջք (stochastic gradient descent): Ավելի խորը հասկանալու համար առկա են նաև քննարկումներ այն մասին, թե ինչպես կարելի է ինտուցիա կառուցել և կարողանալ հասկանալ նեյրոնային ցանցերի ներքին աշխատանքը:
Պերսեպտրոններ
Ի՞նչ է նեյրոնային ցանցը: Սկզբում կդիտարկենք արհեստական նեյրոնի մի տարատեսակ, որ կոչվում է պերսեպտրոն: Պերսեպտրոնները ստեղծվել են 1950-1960-ականներին Ֆրանկ Ռոզենբլատի կողմից՝ ոգեշնչված Ուորեն ՄակԿուլոքի և Վալտեր Փիթսի ավելի վաղ կատարված աշխատանքով: Այսօր ավելի հաճախ օգտագործում են արհեստական նեյրոնների այլ մոդելներ․ այս գրքում և նեյրոնային ցանցերի վերաբերյալ ժամանակակից աշխատանքների մեծամասնության մեջ օգտագործվող նեյրոնների հիմնական մոդելը կոչվում է սիգմոիդ նեյրոն: Մենք շուտով կանդրադառնանք սիգմոիդ նեյրոններին: Բայց որպեսզի հասկանանք, թե ինչու են սիգմոիդ նեյրոնները սահմանվում այնպես, ինչպես սահմանվում են, արժե նախ ժամանակ ծախսել պերսեպտրոնները հասկանալու համար:
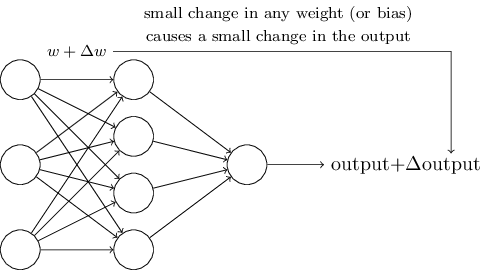
Ինչպե՞ս են աշխատում պերսեպտրոնները: Պերսեպտրոնը մուտքում ստանում է մի քանի երկուական արժեքներ, $x_1, x_2, \ldots$, և ելքում ստանում է մեկ երկուական արժեք (որպես ելք նշանակենք output, այսուհետ այս երկու տերմինները կօգտագործվեն փոխարինաբար)․
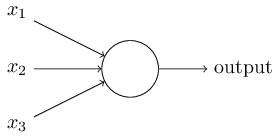
Սա պարզագույն մաթեմատիկական մոդելն է: Դուք կարող եք պերսեպտրոնը հասկանալ որպես մի մեխանիզմ կամ սարք, որը փաստերը կշռելով կայացնում է որոշումներ: Քննարկենք մի օրինակ: Օրինակը այնքան էլ իրատեսական չէ, սակայն հեշտ է հասկանալը, և մենք շուտով կդիտարկենք ավելի իրատեսական օրինակներ: Ենթադրենք մոտենում են հանգստյան օրերը և դուք լսել եք, թե ձեր քաղաքում կայանալու է պանրի փառատոն: Դուք պանիր սիրում եք և խնդիր ունեք որոշելու արդյոք արժի գնալ փառատոնին: Որոշօւմը կայացնում եք հիմնվելով երեք գործոնների վրա․
- Արդյո՞ք եղանակը լավն է,
- Արդյո՞ք ձեր ընկերը կամ ընկերուհին ցանկություն ունեն միանալ ձեզ,
- Արդյո՞ք հնարավոր է փառատոնին հասնել հասարակական տրանսպորտով (ենթադրենք, որ դուք չունեք ավտոմեքենա):
Այժմ ենթադրենք որ դուք պանիր շատ եք սիրում, ընդ որում այնքան շատ, որ պարաստ եք գնալ փառատոնին նույնիսկ եթե ձեր ընկերը կամ ընկերուհին հետաքրքրված չեն և փառատոնին հասնելը դժվար է: Բայց գուցե դուք տանել չեք կարողանում վատ եղանակը և հաստատ չեք մասնակցի փառատոնին, եթե եղանակը անբարենպաստ լինի: Այս բնույթի որոշում կայացնելը մոդելավորելու համար կարող եք օգտագործել պերսեպտրոն: Օրինակ, կարելի է եղանակի համար կշիռը վերցնել որպես $w_1 = 6$, իսկ մյուս պայմանների համար՝ համապատասխանաբար $w_2 = 2$ և $w_3 = 2$: $w_1$-ի մեծ արժեքը ցույց է տալիս, որ եղանակը շատ կարևոր է ձեզ համար՝ շատ ավելի կարևոր է, քան այն փաստը, որ ձեր ընկերը կամ ընկերուհին կմիանան ձեզ կամ հասարակական տրանսպորտի հարմարությունը: Վերջապես, ենթադրենք, որ դուք որպես պերսեպտրոնի շեմ ընտրում եք 5-ը: Շեմի այսպիսի արժեքի դեպքում պերսեպտրոնը կմոդելավորի ձեր որոշում կայացնելու խնդիրը՝ ելքում տալով 1, եթե եղանակը լավն է, և 0, եթե եղանակը բարենպաստ չէ: Հարկ է նկատել, որ վերևում նկարագրած մոդելի դեպքում ձեր ընկերոջ կամ ընկերուհու մասնակցելու ցանկությունը կամ հասարակական տրանսպորտի հարմարությունը «որոշման» ելքի վրա Էապես չեն ազդի:
Կշիռները և շեմը փոփոխելով՝ կստանանք որոշման կայացման տարբեր մոդելներ: Օրինակ, որպես շեմ ընտրենք $3$-ը: Այդ դեպքում պերսեպտրոնը «կորոշի», որ դուք փառատոնին գնաք այն ժամանակ, երբ եղանակը բարենպաստ է կամ երբ փառատոնը մոտ է հասարակական տրանսպորտին և ձեր ընկերը կամ ընկերուհին պատրաստ են միանալ ձեզ: Մի խոսքով դա կդառնա որոշում կայացնելու ուրիշ մոդել: Շեմն իջեցնելը նշանակում է որ դուք ընդհանուր առմամբ հակված եք փառատոնին մասնակցելուն:
Պարզ է, որ պերսեպտրոնը մարդկային որոշում կայացնելու ամբողջական մոդել չէ: Սակայն օրինակը ցույց տվեց թե ինչպես այն կարող է համեմատել տարատեսակ գործոնները որոշում կայացնելու նպատակով: Ավելին, կարծես իրականալի է թվում այն, որ պերսեպտրոնների բարդ կառուցվածքը կարող է անգամ իրականացնել ոչ պարզ որոշումներ:
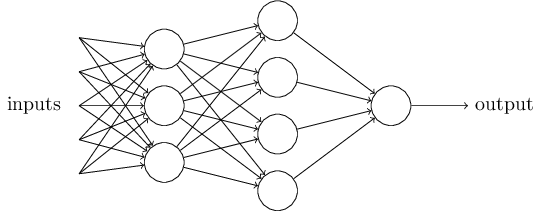
Ի դեպ, պերսեպտրոնի սահմանման մեջ նշել էինք, որ նրանք ունեն մեկ ելքային արժեք: Կարող է տպավորություն ստեղծվել, որ վերևում նկարված ցանցում պերսեպտրոններն ունեն մեկից ավելի ելքեր: Իրականում, մեկից ավել նկարված ելքային սլաքներն ուղղակի նշանակում են, որ տվյալ պերսեպտրոնի ելքը հանդիսանում է մուտք բազմաթիվ այլ պերսեպտրոնների: Այսպիսի նշանակումն ավելի հարմար է դարձնում ցանց նկարելն ու պատկերացնելը:
Փորձենք պարզեցնել պերսեպտրոնի նկարագրությունը: $\sum_j w_j x_j > \mbox{շեմ}$ պայմանը կարելի է պարզեցնել՝ կատարելով երկու փոփոխություն: Առաջին փոփոխությունն է` ներկայացնենք $\sum_j w_j x_j$ գումարը որպես $w \cdot x \equiv \sum_j w_j x_j$ վեկտորների սկալյար արտադրյալ, որտեղ $w$-ն կշիռների վեկտորն է, $x$-ը` մուտքային: Երկրորդ փոփոխությունն է` տանել ելքը անհավասարման մյուս մասը և վերանվանել այն որպես պերսեպտրոնի շեղում` $b \equiv -\mbox{շեմ}$: Օգտագործելով շեղումը շեմի փոխարեն, պերսեպտրոնը կգրենք. \begin{eqnarray} \mbox{ելք} = \left\{ \begin{array}{ll} 0 & \mbox{if } w\cdot x + b \leq 0 \\ 1 & \mbox{if } w\cdot x + b > 0 \end{array} \right. \tag{2}\end{eqnarray} Շեղումը կարելի է հասկանալ որպես մի մեծություն, որը ցույց է տալիս, թե ինչ հեշտությամբ կարելի է այնպես անել, որ պերսեպտրոնը ելքում ստանա $1$ արժեքը կամ կենսաբանորեն՝ շեղումը ցույց է տալիս թե որքան հեշտությամբ կարելի է այնպես անել, որ պերսեպտրոնը հրահանգի: Մեծ շեղումների դեպքում պերսեպտրոնը ելքում $1$ արժեքն ավելի դյուրին է ստանում, քան փոքր շեղումների դեպքում: Պարզ է, որ շեղումը չնչին փոփոխություն է պերսեպտրոնների նկարագրության մեջ, սակայն ավելի ուշ կհամոզվենք, որ դա կբերի էական պարզեցումների: Այդ իսկ պատճառով, այսուհետ կօգտագործենք շեղում տերմինը շեմի փոխարեն:
Պերսեպտրոնները նկարագրել ենք որպես վկայությունների կշռման մեթոդ, որի միջոցով կարելի է կատարել որոշումներ: Սակայն պերսեպտրոնը կարելի է օգտագործել պարզագույն հաշվողական այնպիսի միավորների կառուցման համար, ինչպիսիք են
AND,
OR և
NAND գործողությունները: Օրինակ, ենթադրենք, որ ունենք պերսեպտրոն երկու մուտքերով, ամենքի արժեքը` $-2$, իսկ շեղումը $3$ է: Ահա մեր պերսեպրտոնը.
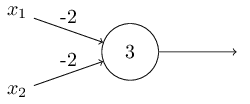
NAND գործողությունը:
NAND-ի օրինակը ցույց է տալիս, որ կարող ենք հասշվել պարզ տրամաբանական ֆունկցիաներ: Իրականում պերսեպտրոնների ցանցի միջոցով կարելի է հաշվել կամայական տրամաբանական ֆունկցիա, քանի որ
NAND-ը ունիվերսալ հաշվողական միավոր է, որով կարելի է կառուցել մնացած գործողությունները: Օրինակ,
NAND-ը կարող ենք օգտագործել գումարման սխեմա կառուցելու համար, որը գումարում է $x_1$ և $x_2$ բիթերը: Սա նշանակում է հաշվել $x_1 \oplus x_2$ բիթ առ բիթ գումարումը և մնացորդային բիթը, որը $1$ է, երբ $x_1$ և $x_2$ բիթերը $1$ են և 0` մնացած դեպքերում:
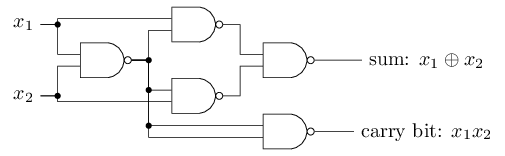
NAND-երը փոխարինենք երկումուտքանի պերսեպտրոններով, յուրաքանչյուրը $-2$ կշռով և $3$ շեղումով: Ահա թե ինչ ցանց է ստացվում: Նկատենք, որ աջ ներքևի
NAND գործողությանը համապատասխանող գագաթը տեղաշարժված է նկարելն ավելի հեշտացնելու նպատակով:
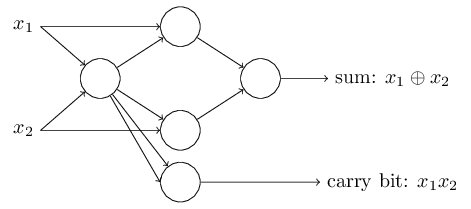
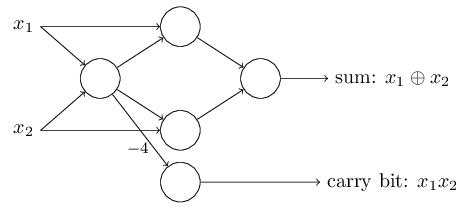
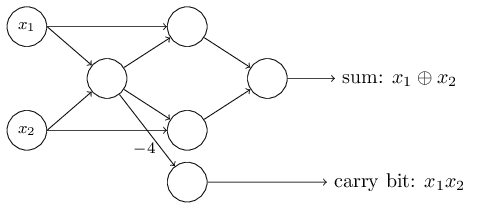
Գումարման գործողության իրականացումը ցույց է տալիս, թե ինչպես կարելի է, օգտագործելով պերսեպտրոնները, բազմաթիվ
NAND գործողություններ պարունակող սխեմա սիմուլացնել: Եվ քանի որ
NAND-երը ունիվերսալ հաշվարկային միավորներ են, ապա հետևում է, որ նույնը ճիշտ է նաև պերսեպտրոնների համար:
Պերսեպտրոնների ունիվրսալ հաշվողունակությունը միժամանակ և՛ հուսադրող է, և՛ հիասթափեցնող: Այն հուսադրող է, քանի որ այն ցույց է տալիս, որ պերսեպտրոնների ցանցը կարող է կամայակն այլ հաշվողական սարքին հավասարաչափ հզոր լինել: Սակայն դա նույնքան հիասթափեցնող
է, քանի որ մյուս կողմից էլ ստացվում է, որ պերսեպտրոնները պարզապես
NAND-ի նոր տեսակ են: Դա այդքան էլ մեծ նորություն չէ:
Այնուամենայնիվ, իրավիճակը շատ ավելի բարվոք է: Պարզվում է, որ հնարավոր է դուրս բերել
սովորող ալգորիթմներ, որոնք ինքնաբերաբար կարող են ձևափոխել արհեստական նեյրոնների կշիռներն ու շեղումները: Այսպիսի ձևափոխումը տեղի է ունենում ի պատասխան արտաքին գործոնների, այլ ոչ ծրագրավորողի նախապես պլանավորված ալգորիթմի հաշվին: Սովորող
ալգորիթմները թույլ են տալիս մեզ օգտագործել արհեստական նեյրոնները էապես տարբեր ձևով, քան արդեն ընդունված տրամաբանական գործողություններն են: Ուղղակիորեն
NAND գործողությունների հերթականություն մշակելու փոխարեն, նեյրոնային ցանցը պարզապես սովորում է լուծել խնդիրներ, երբեմն խնդիրներ, որոնց լուծելու համար ավանդական սխեմա կառուցելը շատ ավելի բարդ կլիներ:
Սիգմոիդ Նեյրոններ
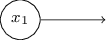
Սովորող ալգորիթմները գաղափարն իհարկե հրաշալի է հնչում: Բայց ինչպե՞ս կարող ենք դուրս բերել նմանատիպ ալգորիթմներ նեյրոնային ցանցերի համար: Ենթադրենք ունենք պերսեպտրոնների ցանց, որը կուզենայինք օգտագործել որոշակի խնդիր լուծելու նպատակով: Օրինակ, որպես մուտքային տվյալներ կարող են հանդիսանալ ձեռագիր թվանշանի թվային ձևաչափով պատկերի պիքսելները: Ընդ որում մեր նպատակն է, որ ցանցը սովորի կշիռներն ու շեղումները այնպես, որ ելքում ստանանք թվանշանների դասակարգումը: Որպեսզի հասկանանք, թե ինչպես կարող է ուսուցումն աշխատել, ենթադրենք, որ ցանցում կշռի կամ շեղման մեջ կատարել ենք փոքրիկ փոփոխություն: Այս փորձի նախընտրելի արդյունքն այն կլիներ, որ այդ փոքր փոփոխությունը հանգեցներ փոկր փոփոխության ցանցի ելքում: Ինչպես շուտով կհամոզվենք, դա է այն հատկությունը, որն ուսուցումը հնարավոր է դարձնում: Սխեմատիկորեն, ահա այն է ինչ անհրաժեշտ է մեզ (ակնհայտ է, որ այս ցանցը չափազանց պարզ է ձեռագիր թվանշաններ ճանաչելու համար).
Եթե կշռի կամ շեղման փոքր փոփոխության հետևանքով ելքում փոքր փոփոխություն առաջանար, ապա մենք կկարողանայինք օգտագործել այդ փաստը կշիռներն ու շեղումները փոփոխելու համար այնպես, որ ցանցը ստանար մեզ համար ցանկալի վարքագիծ: Օրինակ, ենթադրենք ցանցը "9" սխալմամբ թվանշանը ճանաչում է որպես "8": Մենք կարող ենք շեղման և կշիռների համար գտնել մի այնպիսի փոփոխություն, որ ցանցը փոքր ինչ ավելի մոտենա թվանշանը որպես "9" ճանաչելուն: Այնուհետև կարող ենք կրկնել այս քայլը այնքան մինչև ստանանք ավելի և ավելի նպատակահարմար ելքեր: Այսպիսով կասենք, որ ցանցը ուսուցանում է
Խնդիրը կայանում է նրանում, որ վերևում նկարագրվածը պերսեպտրոնների դեպքում տեղի չի ունենում: Իրականում, երբեմն մեկ պերսեպտրոնի կշիռների և շեղման չնչին փոփոխությունը կարող է հանգեցնել ելքի կտրուկ փոփոխության՝ $0$-ից $1$: Այս փոփոխությունը կարող է հանգեցնել ցանցի մնացած հատվածներում բավականին կոմպլեքս փոփոխություններ: Այսպիսով, անգամ եթե 9 ճշտորեն ճանաչվի, ապա վարքագիծը այլ մուտքերի դեպքում կարող է անկառավարելիորեն փոխվել: Այդ իսկ պատճառով կշիռների և շեղման փոքրիկ փոփոխությամբ ցանցի վարքագիծը փոխելով նպատակին մոտենալը դառնում է բավականին գրեթե անհնար: Կարող է այս խնդիրը շրջանցելու խելացի միջոց գոյություն ունի, սակայն միանգամից ակնհայտ չէ, թե ինչպես կարող ենք սովորեցնել պերսեպտրոնների ցանցին:
Մենք կարող ենք շրջանցել այս խնդիրը՝ ներմուծելով նոր տեսակի արհեստական նեյրոն, որը կոչվում է սիգմոիդ նեյրոն: Սիգմոիդ նեյրոնները նման են պերսոտրոններին, սակայն փոփոխված են այնպես, որ կշռի կամ շեղման փոքր փոփոխություններիը առաջացնում են փոքր փոփոխություններ ելքում: Սա է այն պայմանը, որի դեպքում սիգմոիդ նեյրոնների ցանցը կկարողանա սովորել:
Նկարագրենք սիգմոիդ նեյրոնը: Կպատկերենք այն այնպես ինչպես պատկերել էինք պերսեպտրոնը.
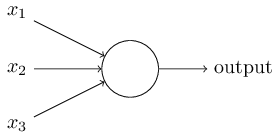
Սիգմոիդ նեյրոնները կարող են առաջին հայացքից տարբեր թվալ պերսեպտրոններից: Իսկ եթե ծանոթ չեք ֆունկցիայի հետ, ապա սիգմոիդի տեսքը կարող է նաև ակնհայտ չլինել: Իրականում, պերսեպտրոնների և սիգմոիդ նեյրոնների միջև կան բազմաթիվ նմանություններ:
Որպեսզի հասկանանք այդ նմանությունները, ենթադրենք $z$-ը բավականին մեծ դրական թիվ է՝ ներկայացված հետևյալ տեսքով` $z \equiv w \cdot x + b$: Հետևաբար, $e^{-z} \approx 0$ և $\sigma(z) \approx 1$: Այլ կերպ ասած, եթե $z = w \cdot x+b$ մեծ դրական թիվ է, ապա սիգմոիդ նեյրոնի արժեքը մոտավոր $1$ է (այնպես, ինչպես կլիներ պերսեպտրոնի դեպքում): Մյուս կողմից, ենթադրենք, որ $z = w \cdot x+b$ շատ փոքր բացասական թիվ է, ապա $e^{-z} \rightarrow \infty$ և $\sigma(z) \approx 0$, հետևաբար, եթե $z = w \cdot x +b$ շատ փոքր բացասական թիվ է, ապա սիգմոիդի արժեքը ձգտում է պերսեպտրոնի արժեքին: Միայն $w \cdot x+b$-ի ոչ մեծ բացարձակ արժեքների դեպքում է, որ սիգմոիդի և պերսեպտրոնի մոդելները տարբերվում են:
Իսկ ի՞նչ տեսք ունի $\sigma$-ն: Ինչպե՞ս հասկանանք այն: Իրականում $\sigma$-ի ճշգրիտ արժեքն էական չէ, էական է այն, թե ինչ տեսք ունի ֆունկցիայի գրաֆիկը: Ահա այն.
Սա քայլ ֆունկցիայի (step function) «հարթեցված» տարբերակն է:
Եթե $\sigma$-ն լիներ քայլ ֆունկցիան, ապա սիգմոիդ նեյրոնը կլիներ պերսեպտրոնը, քանի որ ելքում կստացվեին $1$ կամ $0$ արժեքները՝ կախված նրանից, թե $w\cdot x+b$ դրական է, թե բացասական*: *Իրականում, $w \cdot x +b = 0$ պերսեպտրոնի արժեքը $0$ է, երբ քայլ ֆունկցիայի արժեքը $1$ է: Այսպիսով, ճշգրիտության համար նշեմ, որ քայլ ֆունկցիայի արժեքը այդ կետում կարիք կլինի փոխել: Այնուամենայնիվ, կարծում եմ ընդհանուր գաղափարը պարզ է: Օգտագործելով $\sigma$ ֆունկցիան, մենք ստանում ենք պերսեպտրոնի փոքր-ինչ հարթեցված տարբերակը, ինչն ամենակարևորն է, քանի որ դա նշանակում է, որ կշռի $\Delta w_j$ և շեղման $\Delta b$ փոքր փոփոխությունների արդյունքում վերջնական արժեքի փոփոխությունը $\Delta \mbox{ելք}$–ը նույնպես փոքր կլինի: Ըստ էության, $\Delta \mbox{ելք}$-ը կարելի է մոտարկել հետևյալ կերպ \begin{eqnarray} \Delta \mbox{ելք} \approx \sum_j \frac{\partial \, \mbox{ելք}}{\partial w_j} \Delta w_j + \frac{\partial \, \mbox{ելք}}{\partial b} \Delta b, \tag{5} \end{eqnarray} որտեղ գումարն ըստ բոլոր $w_j$ կշիռների է, իսկ $\partial \, \mbox{ելք} / \partial w_j$ և $\partial \, \mbox{ելք} /\partial b$ ելքի մասնակի ածանցյալներն են ըստ $w_j$ և $b$ փոփոխականների համապատասխանաբար: Խնդրում եմ խուճապի չմատնվել, եթե մասնակի ածանցյալները հարմարավետ չեն ձեզ համար: Կարող է թվալ, որ վերևի արտահայտությունը բարդ է, սակայն այն ուղղակի նշանակում է, որ $\Delta \mbox{ելք}$-ը գծային ֆունկցիա է $\Delta w_j$ և $\Delta b$ կշիռների և շեղման փոփոխություններից կախված: Գծայնությունը թույլ է տալիս հեշտությամբ ընտրել կշիռների և շեղումների փոքր փոփոխություն այնպես, որ հանգեցնի փոքր փոփոխություն ելքում: Այսպիսով սիգմոիդները, ունենալով պերսեպտրոններին նման որակական հատկանիշներ, միաժամանակ թույլ են տալիս հեշտությամբ հասկանալ, թե կշիռների և շեղման փոփոխությունը ինչպիսի ազդեցություն կունենա նեյրոնի ելքի վրա:
Քանի որ ավելի մեծ կարևորություն ենք տալիս $\sigma$ ֆունկցիայի գրաֆիկի տեսքին, քան ինքնին ֆունկցիային, ապա ինչու՞ օգտագործենք $\sigma$-ի (3) -ում տրված տեսքը: Ավելի ուշ մենք կտեսնենք այնպիսի նեյրոններ, որոնց արժեքը $f(w \cdot x + b)$ որոշվում է այլ $f(\cdot)$ ակտիվացման ֆունկցիայի (activation function) միջոցով: Ակտիվացման ֆունկցիայի փոփոխության հետևանքով (5) հավասարման մեջ կարող են փոխվել միայն մասնակի ածանցյալների արժեքները: Հեշտ է նկատել նաև, որ վերոնշյալ մասնակի ածանցյալները հաշվելիս $\sigma$ ֆունկցիան հաշվման գործընթացը կհեշտացնի, քանի որ էքսպոնենցիալ ֆունկցիաները դիֆերենցելիս հրաշալի հատկություններ ունեն։ Այնուամենայնիվ, $\sigma$-ն բավականին տարածված է նեյրոնային ցանցերում որպես ակտիվացման ֆունկցիա, և մենք այն բավականին հաճախ կօգտագործենք այս գրքում:
Իսկ ինչպե՞ս պետք է մեկնաբանել սիգմոիդ նեյրոնի ելքը (արժեքը): Հեշտ է նկատել, որ համեմատած պերսեպտրոնին, սիգմոիդ նեյրոնի ելքում միայն $0$ կամ $1$ չէ, այլ $0$-ից $1$ միջակայքում գտնվող արժեքներ (օրինակ $0.173\ldots$ կամ $0.689\ldots$ և այլն): Այդ հատկությունը կարելի է օգտագործել բազմաթիվ ձևերով: Օրինակ, այն կարելի է օգտագործել ելքային արժեքը որպես նկարի (որպես նեյրոնային ցանցին մուտքային արժեքներ) պիքսելների միջին ինտենսիվություն ներկայացնելու համար: Սակայն երբ նպատակը ելքը բինար արժեքով ներկայացնելն է (օրինակ մուտքային նկարը "9" է կամ "9" չէ), ապա այդ դեպքում կարելի է օգտագործել այլ մարտավարություն` եթե արժեքը $0.5$-ից փոքր է, ապա "9" է և համապատասխանաբար "9" չէ երբ ելքի արժեքը $0.5$-ից փոքր չէ: Նմանատիպ պայմանավորվածությունները հստակ կնշվեն գրքի հետագա քննարկումներում, որպեսզի շփոթություն չառաջանա:
Վարժություններ
-
Պերսեպտրոն սիմուլյացնող սիգմոիդ նեյրոններ, մաս I $\mbox{}$
Ենթադրենք, որ պերսեպտրոններից կազմված ցանցի բոլոր շեղումները և կշիռները բազմապատկում ենք $c > 0$ դրական հաստատունով: Ցույց տվեք, որ ցանցի վարքագիծը դրանից չի փոխվում: -
Պերսեպտրոն սիմուլյացնող սիգմոիդ նեյրոններ, մաս II $\mbox{}$
Դիտարկենք պերսեպտրոնների ցանց: Ենթադրենք ցանցի մուտքն արդեն ընտրված է: Ընդ որում մուտքային արժեքն էական չէ, այլ էական է այն, որ այն ֆիքսված է: Ենթադրենք կշիռներն ու շեղումները բավարարում են $w \cdot x + b \neq 0$ պայմանին $x$ մուտքի և ցանցի կամայական պերսեպտրոնի համար: Այժմ ցանցի բոլոր պերսեպտրոնները փոխարինենք սիգմոիդ նեյրոններով և բազմապատկենք կշիռներն ու շեղումները $c > 0$ հաստատունով: Ցույց տվեք, որ երբ $c \rightarrow \infty$, ապա սիգմոիդ նեյրոնների ցանցի վարքագիծը նույնն է, ինչ պերսեպտրոններից կազմված ցանցինը: Բացատրեք, թե ինչպես վերոնշվածը կարող է տեղի չունենալ, երբ գոյություն ունի պերսեպտրոն, որի համար $w \cdot x + b = 0$ պայմանը չի բավարարվում:
Նեյրոնային ցանցերի կառուցվածքը
Հաջորդ բաժնում կներկայացնենք նեյրոնային ցանց, որը բավականին հաջողությամբ կարողանում է դասակարգել ձեռագիր թվանշանները: Որպես նախապատրաստական աշխատանք, դիտարկենք որոշ տերմիններ, որը մեզ թույլ կտա անվանումներ տալ ցանցի բաղադրիչներին: Ենթադրենք, որ ունենք որևէ ցանց.
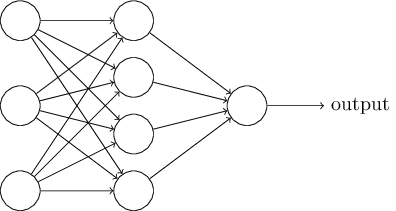
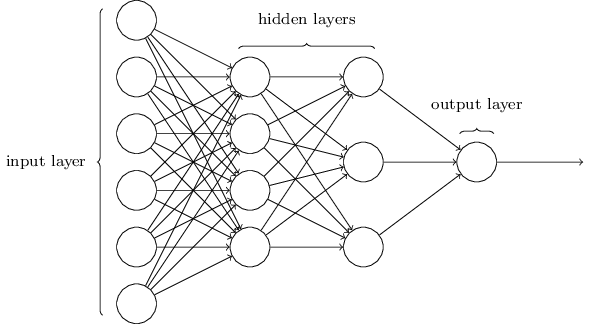
Կախված խնդրից՝ մուտքային և ելքային շերտերի կառուցվածքները հիմնականում ակնհայտ են լինում: Ենթադրենք, որ ցանկանում ենք պարզել արդյո՞ք ձեռագիր թվանշանը ցույց է տալիս "9" թիվը: Ցանցը կառուցելու բնական մեթոդը կլինի պատկերի պիքսելների խտության արտապատկերումը մուտքային նեյրոններին: Եթե պատկերը $64$-ը $64$-ի վրա անգույն նկար է, այդ դեպքում կունենանք $4,096 = 64 \times 64$ մուտքային նեյրոններ, որտեղ խտությունները նորմալիզացված են $0$-ից $1$ միջակայքում: Ելքային շերտը կպարունակի միայն մեկ նեյրոն, որի արժեքի $0.5$-ից մեծ լինելը կնշանակի, որ նկարը 9 է, իսկ փոքր լինեու դեպքպւմ` 9 չէ:
Մինչդեռ նեյրոնային ցանցի մուտքային և ելքային շերտերի կառուցվածքը սովորաբար ակնհայտ է, ապա թաքնված շերտերի կառուցվածքը կարող է էապես բարդ լինել: Հատկապես հնարավոր չէ թաքնված շերտերի նախագծման պրոցեսը մի քանի պարզ ինտուիտիվ կանոններով նկարագրել։ Փոխարենը նեյրոնային ցանցերի հետազոտողները ստեղծել են բազմաթիվ փորձարարական կառուցվածքներ, մոտեցումներ, որոնք օգնում են մարդկանց ցանցերից ստանալ իրենց համար ցանկալի վարքագիծը: Ավելի ուշ, գրքում կհանդիպենք այդպիսի կառուցվածքներից մի քանիսին։
Մինչ այժմ մենք քննարկում էինք այնպիսի նեյրոնային ցանցեր, որոնցում մի շերտի ելքն օգտագործվում է որպես մուտք հաջորդ շերտի համար: Այդպիսի ցանցերը կոչվում են առաջաբեր(feedforward) նեյրոնային ցանցեր: Սա նշանակում է, որ ցանցում չկան ցիկլեր. ինֆորմացիան միշտ առաջ է բերվում և ոչ մի դեպքում՝ ետ: Եթե թույլատրեինք ցիկլեր, ապա կստացվեր, որ $\sigma$-ի մուտքը կախված կլիներ ելքից, այդ պատճառով այդպիսի ցիկլեր թույլ չենք տալիս։
Սակայն գոյություն ունեն այնպիսի նեյրոնային ցանցեր, որոնց մեջ ցիկլերը հնարավոր են: Այդպիսի մոդելները կոչվում են ռեկուրենտ նեյրոնային ցանցեր: Գաղափարը կայանում է նրանում, որ այդ կառուցվածքներում նեյրոնը աշխատում է որոշակի սահմանափակ ժամանակի ընթացքում՝ մինչև պասիվանալը: Այդ աշխատանքը կարող է այլ նեյրոններին խթանել, որպեսզի իրենք էլ սկսեն աշխատել որոշակի ժամանակ անց՝ ինչ-որ չափավոր ժամանակով: Վերջինս իր հերթին հանգեցնում է նոր նեյրոնների աշխատանքին, այսպիսով հանգեցնելպվ նեյրոններ կասկադային աշխատանքի: Ցիկլերն այս դեպքում ոչնչի վրա չեն ազդում, քանի որ նեյրոնի ելքը ազդեցություն ունի մուտքի վրա որոշ ժամանակ անց, այլ ոչ անմիջապես:
Ռեկուրենտ նեյրոնային ցանցերը հետազոտությունները ժամանակի ընթացքում աճում են, հետևաբար աճում են նաև կիրառությունները: Այս տեսակի ցանցերն, ըստ էության, ավելի մոտիկ են ուղեղի աշխատանքի մոդելին, քան առաջաբեր ցանցերը: Ռեկուրենտ ցանցերն ունակ են լուծելու այնպիսի խնդիրներ, որոնք առաջաբեր ցանցերի համար մեծ դժվարություն են ներկայացնում: Այնուամենայնիվ, սահմանափակելով մեր շրջանակը, այս գրքում կկենտրոնանք ավելի լայնորեն կիրառվող առաջաբեր ցանցերի վրա:
Պարզ ցանց ձեռագիր թվանշանների ճանաչման համար
Վերադառնանք ձեռագիր թվանշանների ճանաչման խնդրին: Բաժանենք խնդիրը երկու ենթախնդիրների: Առաջինը, բաժանենք բազմաթիվ նկարներ պարունակող պատկերը մեկական թվանշան պարունակող նկարների հերթականության: Օրինակ, մեր նպատակն է բաժանել հետևյալ պատկերը.
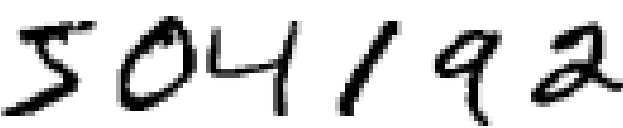
6 առանձին պատկերների,

մարդիկ բավականին հեշտությամբ լուծում են այս սեգմենտացիայի խնդիրը, սակայն նույն խնդիրը համակարգչային ծրագրի համար բնավ հեշտ չէ լուծելը: Նկարը մասնատելուց հետո ծրագիրը պետք է տարբերակի յուրաքանչյուր առանձին թվանշան: Օրինակ կցանկանայինք, որ մեր ծրագիրը վերևի թվերից առաջինը ճանաչեր որպես 5.
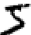
Ուշադրությունը սևեռենք թվարկված խնդիրներից երկրորդին՝ առանձին թվանշանների տարբերակմանը։ Պարզվում է, որ բաժանման խնդիրն այդքան էլ դժվար չէ լուծելը, եթե գիտենք թվանշանների տարբերակման լավ լուծում, այդ իսկ պատճառով կդիտարկենք միայն տարբերակման խնդիրը։ Բաժանման խնդիրը լուծելու բազմաթիվ մոտեցումներ կան: Մոտեցումներից մեկն է` փորձել տարբեր ձևերով բաժանել և թույլ տալ, որպեսզի թվանշաններ ճանաչող ծրագիրը գնահատականներ տա բաժանումներին: Բաժանումը գնահատվում է՝ կախված նրանից, թե թվանշան տարբերակող ծրագիրն ինչքան է "վստահ" բաժանվածի բոլոր մասերում տարբերակված թվանշանների հարցում, ընդ որում` որքան շատ են այն բաժինները, որում տարբերակումը վստահ չէ, այնքան ավելի ցածր է գնահատականը: Գաղափարը կայանում է նրանում, որ եթե տարբերակող ծրագիրը դժվարությամբ է տարբերակում գոնե մեկ բաժնում, ապա դրա պատճառն ամենայն հավանականությամբ սխալ բաժանման մեջ է կայանում: Ընդ որում սա եղանակներից մեկն է, թե ինչպես կարելի է լուծել բաժանման խնդիրը: Այդ իսկ պատճառով, բաժանման խնդրի փոխարեն մենք կկենտրոնանանք թվանշաններ ճանաչելու համար նախատեսված նեյրոնային ցանց նախագծելու վրա:
Թվանշան ճանաչելու նպատակով մենք կկառուցենք եռաշերտ նեյրոնային ցանց.
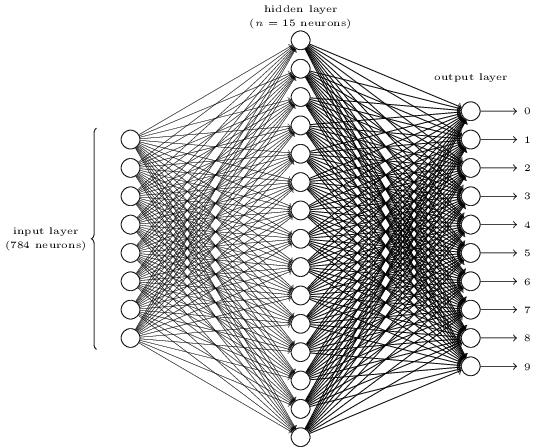
Ցանցի մուտքային շերտը պարունակում է կոդավորված մուտքային պիքսելները: Ինչպես քննարկվում է հաջորդ բաժնում, ուսուցման տվյալներն իրենցից ներկայացնում են $28$ պիքսել երկարությամբ և լայնությամբ ձեռագիր թվանշանների պատկերներ, հետևաբար մուտքային շերտը պարունակում է $784 = 28 \times 28$ նեյրոններ: Պարզության համար, վերևի գծանկարում $784$ նեյրոններից շատերը բաց են թողնված: Մուտքային պիքսելները մոխրագույն են, այնպես, որ $0.0$-ն ներկայացնում է սպիտակը իսկ $1.0$-ը` սևը, իսկ այդ միջակայքում գտնվող արժեքները ներկայացնում են մոխրագույնի աստիճանաբար մգացող երանգները:
Ցանցի երկրորդ շերտը թաքնված է: Երկրորդ շերտի նեյրոնների քանակը նշանակենք $n$, որի արժեքի շուրջ կկատարենք բազմաթիվ փորձեր: Օրինակը ներկայացնում է համեմատաբար փոքր թաքնված շերտ, որը պարունակում է $n = 15$ նեյրոններ:
Ցանցի ելքային շերտը պարունակում է 10 նեյրոններ: Եթե առաջին նեյրոնի արժեքը, օրինակ $\approx 1$ (մոտ է 1-ին), ապա դա նշանակում է, որ ցանցը կարծում է, որ թվանշանը $0$ է: Երբ երկրորդ նեյրոնն ունի այդ հատկությունը, ապա դա կնշանակի, որ ցանցը կարծում է՝, որ թվանշանը $1$ է և այդպես շարունակ: Այսպիսով, մենք ելքային նեյրոնները համարակալում ենք $0$-ից $9$ և պարզում, թե որ նեյրոնն ունի մեծագույն ակտիվացիայի արժեքը: Եթե այդ նեյրոնը, ենթադրենք, $6$-ն է, ապա ցանցը ցույց է տալիս, որ թվանշանը $6$-ն է և այդպես շարունակ:
Հարց է առաջանում, թե ինչու ենք օգտագործում $10$ ելքային նայրոններ: Վերջիվերջո ցանցի նպատակն է ցույց տալ, թե ($0, 1, 2, \ldots, 9$) թվանշաններից որին է համապատասխանում մուտքային նկարը: Թվում է, թե բնական է օգտագործել ելքային $4$ նեյրոն, որոնցից յուրաքանչյուրը կունենա բինար արժեք` կախված նրանից, թե $0$-ից $1$ միջակայքի որ մասում է արժեքը: Չորս նեյրոնները բավարար են պատասխանը կոդավորելու հանար, քանի որ $2^4 = 16$, որը մեծ է 10 հնարավոր արժեքների քանակից: Ինչու՞ է մեր ցանցը փոխարենը $10$ նեյրոն օգտագործում: Մի՞թե դա անէֆֆեկտիվ չէ: Պատասխանը փորձարարական է. իրականում կարելի է փորձել երկու ձևերով էլ: Պարզվում է, որ հենց այս խնդիրը $10$ ելքային նեյրոններով ավելի լավ է սովորում թվանշանները ճանաչել, քան $4$ ելքային նեյրոններով: Այնումամենայնիվ, մեզ հետաքրքիր է, թե ինչու է $10$ ելքերով ցանցն աշխատում ավելի լավ: Հնարավո՞ր է արդյոք նախորոք որոշել, թե $10$ կամ $4$ է պետք օգտագործել:
Որպեսզի պարզենք, թե ինչու ենք այդպես վարվում, փորձենք հասկանալ, թե ինչպես է աշխատում նեյրոնային ցանցը: Ենթադրենք օգտագործում ենք $10$ ելքային նեյրոններ: Դիտարկենք առաջին ելքային նեյրոնը, որը պատասխանատու է որոշելու նկարի $0$ լինելու որոշման համար: Դա տեղի է ունենում թաքնված շերտերից ստացված «վկայությունները» «համեմատելով»: Ինչպե՞ս են աշխատում թաքնված շերտերը: Ենթադրենք թաքնված շերտի առաջին նեյրոնը որոշում է արդյոք ներքևում նշված նկարն առկա է, թե ոչ:

Դա կարելի է անել մուտքային պիքսելներին, որոնք հատվում են նկարին համապատասխանող պիքսելների ծանր կշիռներ տալով և համեմատաբար թեթև կշիռներ տալով մնացած մոտքային պիքսելներին: Նույն ձևով, ենթադրենք, որ երկրորդ, երրորդ և չորրորդ նեյրոնները թաքնված շերտում որոշում են արդյոք հետևյալ նկարները ազատ են:

Ակնհայտ է, որ այդ չորս նկարները միասին կազմում են $0$ նկարը: earlier:

Այսպիսով, եթե թաքնված նեյրոնների բոլոր 4 նեյրոնները աշխատում են, ապա եզրակացնում ենք, որ թվանշանը մոտ է $0$-ին: Իհարկե դա միակ միակ վկայությունը չէ, որից կարող ենք եզրակացնել, որ թվանշանը $0$-ն է: Մենք կարող ենք օրինականորեն ստանալ $0$ բազմաթիվ այլ ձևերով (օրինակ վերևի նկարների նկատմամբ փոփոխություններ կատարելով):
Ենթադրելով, որ նեյրոնային ցանցն աշխատում է այսպես, ըստ էության կարող ենք խելամիտ բացատրություն տալ, թե ինչու նպատակահարմար է օգտագործել $10$ ելք $4$-ի փոխարեն: Եթե ունենայինք $4$ ելքեր, ապա առաջին ելքային նեյրոնը փորձելու էր որոշելու թվանշանի առաջին բիթը: Նկատենք, որ առաջին բիթը վերևում տրված պարզ նկարի հետ կապելու «հեշտ» ձև չկա:
Այսպիսով, այս ամենը ոչ ճշգրիտ է: Ոչնչից չի հետևում, որ պարզ եռաշերտ նեյրոնային ցանցը պարտավոր է աշխատել նկարագրված ձևով` թաքնված շերտերը գուշակելով պարզ կոմպոնենտների տեսքերը: Հնարավոր է, որ խելոք սովորող ալգորիթմը գտնի կշիռների այնպիսի դասավորվածություն, որը թույլ տա օգտագործել $4$ ելքային նեյրոններ:
Վարժություն
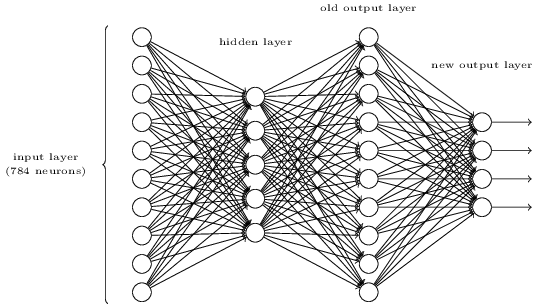
- Գոյություւն ունի մոտեցում, որը հնարավորություն է տալիս գտնել թվի երկակի(բիթային) ներկայացումը վերևում նշված ցանցին ևս մեկ շերտ ավելացնելով: Նոր շերտը նախորդ շերտի արժեքը փոխակերպում է բինար ներկայացման ինչպես ներկայացված է ներքևում: Գտնել նոր ելքային շերտի կշիռներն ու շեղումները: Կարող եք ենթադրել, որ նեյրոնների առաջին $3$ շերտերն այնպիսին են, որ երրորդ շերտից ճիշտ արժեքը ունի ամենաքիչը $0.99$ հավանականություն և ոչ ճշգրիտ արժեքներն ունեն $0.01$-ից փոքր արժեք:
Ուսուցում գրադիենտային վայրէջքի միջոցով
Այժմ, երբ մենք ունենք նեյրոնային ցանցի կառուցվածքը, պարզենք, թե ինչպես այն կարող է սովորել ճանաչել թվանշաններ: Առաջինը, ինչ մեզ պետք է, դա ուսուցման համար նախատեսված տվյալների բազմությունն է (ուսուցման տվյալների բազմություն): Մենք կօգտագործենք MNIST տվյալների բազմությունը, որը պարունակում է տաս հազարավոր ձեռագիր թվանշանների նկարներ իրենց ճշգրիտ թվային պիտակներով: MNIST անունը գալիս է նրանից, որ այն Միացյալ Նահանգների NIST-ի (National Institute of Standards and Technology) կողմից հավաքագրված երկու տվյալների բազմությունների փոփոխության ենթարկված (Modified) տարբերակն է: Ահա մի քանի նկարներ MNIST-ից:

Ինչպես տեսնում եք, այս թվանշաններն, ըստ էության, նույնն են, ինչ ցույց էր տրված գլխի սկզբում որպես ճանաչման խնդիր: Իհարկե, ցանցը սովորեցնելուց կփորձարկենք նկարների վրա, որոնք մարզման տվյալների բազմությունում չկան:
MNIST-ի տվյալները բաղկացած են երկու մասից: Առաջին մասը պարունակում է 60,000 նկարներ, որոնք կօգտագործվեն որպես մարզման տվյալներ (training data): Այդ նկարները 250 մարդկանց սկանավորված ձեռագիր թվանշաններ են այնպես, որ մարդկանցից կեսը Միացյալ Նահանգների մարդահամարի բյուրոյի աշխատակիցներն են, մյուս կեսը՝ ավագ դպրոցի աշակերտներ: Նկարները մոխրագույն են և 28-ը 28-ի վրա: MNIST տվյալների բազմության երկրորդ մասը 10,000 նկարներից է բաղկացած, որը կօգտագործվի որպես թեստային տվյալներ: Այստեղ նույնպես նկարները մոխրագույն են և 28-ը 28-ի վրա: Թեստային տվյալները կօգտագործենք, որպեսզի գնահատենք, թե ինչքան լավ է մեր նեյրոնային ցանցը սովորել թվանշանների ճանաչումը: Որպեսզի թեստավորումը լավը լինի, թեստային տվյալների բազմությունը վերցված է 250 ուրիշ մարդկանց բազմությունից: Սա մեզ վստահություն է տալիս, որ համակարգը կարող է ճանաչել այն մարդկանց ձեռագրերը, որոնք նախկինում չի հանդիպել մարզման ժամանակ:
Ուսուցման մուտքը նշանակենք $x$-ով: Ընդ որում մուտքային $x$ վեկտորը $28 \times 28 = 784$ չափանի վեկտոր է,որի ամեն անդամը ներկայացնում է մեկ պիքսելի մոխրագույն արժեքը: Նշանակենք համապատասխան ելքային արժեքը $y = y(x)$, որտեղ $y$-ը $10$ չափանի վեկտոր է: Օրինակ, եթե որոշակի ուսուցման վեկտորը ներկայացնում է 6 թվանշանը, ապա $y(x) = (0, 0, 0, 0, 0, 0, 1, 0, 0, 0)^T$ ցանցի ցանկալի ելքային վեկտորն է, որտեղ $T$-ն տրանսպոնացման գործողությունն է (որը տողային վեկտորը վերածում է սյունակային վեկտորի և հակառակը):
Մեր նպատակն է գտնել մի ալգորիթմ, որը հնարավորություն է տալիս հաշվել այնպիսի կշիռներ և շեղումներ, որ ցանցի ելքային արժեքը մոտարկի $y(x)$-ը բոլոր $x$ մուտքային արժեքների դեպքում: Որպեսզի հաշվարկենք, թե որքան մոտ ենք «մոտարկման նպատակին», սահմանենք գնի ֆունկցիա (cost function)* *Երբեմն հղվում են որպես կորստի (loss) կամ նպատակային (objective) ֆունկցիա: Մենք օգտագործում ենք գնի ֆունկցիա տերմինը այս գրքում, սակայն խորհուրդ է տրվում հաշվի առնել, որ նշված ալտերնատիվ տերմինները նույնպես լայն օգտագործում ունեն, հատկապես գիտական հոդվածներում: : \begin{eqnarray} C(w,b) \equiv \frac{1}{2n} \sum_x \| y(x) - a\|^2. \tag{6}\end{eqnarray} Որտեղ $w$-ով նշանակված է ցանցում բոլոր կշիռների բազմությունը, $b$-ով նշանակված են բոլոր շեղումները, $n$-ը ուսուցման մուտքերի քանակն է, $a$-ն ցանցի ելքային վեկտորն է $x$ մուտքի դեպքում և գումարը բոլոր մուտքային $x$-երով է: Իհարկե, $a$ ելքային արժեքը կախված է $x$-ի, $w$-ի and $b$-ի արժեքներից, սակայն պարզությունը պահելու համար, այդ կախվածությունը նշված չէ բանաձևում: $\| v \|$ նշանակումը ցույց է տալիս $v$-ի երկարության ֆունկցիան: $C$-ն կոչենք քառակուսային գնի ֆունկցիա. այն հայտնի է նաև որպես Միջին Քառակուսային Սխալ: Դիտարկելով քառակուսային գնի ֆունկցիան, եզրակացնում ենք, որ $C(w,b)$-ն ոչ բացասական է, քանի որ յուրաքանչյուր անդամը ոչ բացասական է: Ավելին, $C(w,b)$ արժեքը փոքրանում է (օրինակ $C(w,b) \approx 0$), երբ $y(x)$-ի արժեքը մոտենում է ելքային $a$ արժեքին բոլոր $x$ ուսուցման մուտքերի համար: Այսպիսով, կարելի է ասել, որ ալգորիթմը լավ է աշխատում, երբ այն կարողանում է գտնել կշիռների և շեղումների այնպիսի արժեքներ, որ $C(w,b) \approx 0$: Նմանապես, այն լավ չի աշխատում, երբ $C(w,b)$ մեծ արժեք ունի, ինչը նշանակում է $y(x)$ մոտիկ չէ $a$ ելքերին, մեծ քանակությամբ արժեքների դեպքում: Այսպիսով, մեր ուսուցման ալգորիթմի նպատակն է լինելւ մինիմիզացնել $C(w,b)$ արժեքը որպես ֆունկցիա կշիռներից և շեղումներից: Այսպիսով, մենք ուզում ենք գտնել այնպիսի կշիռների և շեղումների բազմություն, որը արժեքը դարձնում է ինչքան հնարավոր է փոքր: Մենք դա կիրականացնենք՝ օտգագործելով գրադիենտային վայրէջքի (gradient descent) ալգորիթմը:
Ինչու՞ դիտարկել քառակուսային գինը, չէ՞ որ մեր վերջնական նպատակն է ունենալ մեծ քանակությամբ նկարներ՝ ճիշտ տարբերակված ցանցի կողմից: Ինչու՞ չմաքսիմիզացնել ճիշտ գուշակված նկարների քանակը, փոխարենը դիտարկելու այնպիսի մի միջանկյալ մեծություն ինչպիսին է քառակուսային արժեքը: Խնդիրը կայանում է նրանում, որ ճիշտ տարբերակված նկարների քանակի ֆունկցիան կախված ցանցի կշիռներից և շեղումից այնքան էլ հարմար չէ օպտիմիզացիայի խնդիր լուծելու համար: Այն է` կշիռների և շեղման փոքր փոփոխությունը չի հանգեցնի ոչ մի փոփոխության ճիշտ տարբերակված նկարների քանակի մեջ: Այդ իսկ պատճառով դժվար է հասկանալ, թե ինչպես փոփոխել կշիռներն ու շեղումները, որպեսզի բարելավվի ալգորիթմի կատարողականությունը: Պարզվում է, որ եթե փոխարենը վերցնենք այնպիսի գնի ֆունկցիա, ինչպիսին է քառակուսային գնի ֆունկցիան, կշիռների և սեղումների փոքր փոփոխությունները կհանգեցնեն գնի բարելավման: Այդ իսկ պատճառով, մենք սկզբում կկենտրոնանք գնի ֆունկցիան մինիմիզացնելու վրա, այնուհետև կդիտարկենք տարբերակման ճշտությունը:
Անգամ եթե հայտնի է, որ մեր նպատական է օգտագործել այնպիսի ֆունկցիա, որի հետ հեշտ լինի աշխատել օպտիմիզացիայի առումով, մեկ է, հարց է առաջանում, թե ինչու ենք ընտրում հենց հավասարում (6) -ի քառակուսային ֆունկցիան. Մի գուցե, եթե ընտրեինք այլ ֆունկցիա, կստանայինք մինիմիզացնող կշիռների և շեղումների այլ բազմություն: Սա արդարացված անհանգստություն է, և այդ պատճառով ավելի ուշ ետ կվերադառնանք գնի ֆունկցիային և կկատարենք որոշ փոփոխություններ: Այնուամենայնիվ, հավասարում (6) -ի գնի ֆունկցիան հարմար է և բավարար նեյրոնային ցանցերի հիմնական կոնցեպտները սովորելու համար, հետևաբար, մենք առայժմ դա կօգտագործենք:
Ընդհանրացնելով, մեր նեյրոնային ցանցի մարզման նպատակը կշիռների և շեղումների որոշումն է, որը մինիմիզացնում է $C(w, b)$ քառակուսային ֆունկցիայի արժեքը: Սա բավականին հստակ դրված խնդիր է, սակայն այն պարունակում է բազմաթիվ շեղող մասեր, օրինակ կշիռները, շեղումները, նեյրոնային ցանցի կառուցվածքը և այլն: Պարզվում է, որ եթե արհամարհենք «գնի ֆունկցիայի ծագման պատմությունը» և կենտրոնանանք միայն մինիմիզացիայի վրա մենք կարող ենք բավականին առաջընթաց ունենալ: Ենթադրենք, որ ունենք մեկից ավել փոփոխականներից ֆունկցիա և մեր նպատակն է մինիմիզացնել այդ ֆունկցիան: Մենք կկառուցենք գրադիենտային վայրէջքի (gradient descent) մոտեցումը, որը կօգտագործենք մինիմիզացիայի խնդիրը լուծելու համար: Այնուհետև կվերադառնանք նեյրոնային ցանցերի այն գնի ֆունկցիային, որը մենք նպատակահարմար ենք գտնում մինիմիզացնել:
Այսպիսով, դիտարկենք $C(v)$ ֆունկցիան: Սա կարող է լինել կամայական $v = v_1, v_2, \ldots$ իրական փոփոխականների ֆունկցիա: Նկատենք, որ $w$ և $b$-ն փոխարինվել էին $v$-ով, որպեսզի ցույց տրվի, որ $C$-ն կարող է լինել կամայական ֆունկցիա. մենք նեյրոնային ցանցերի կոնտեքստով այլևս չենք մտածում: $C(v)$-ն մինիմզացնելու համար, ենթադրենք այն երկու փոփոխականի ֆունկցիա է` $C(v_1, v_2)$:
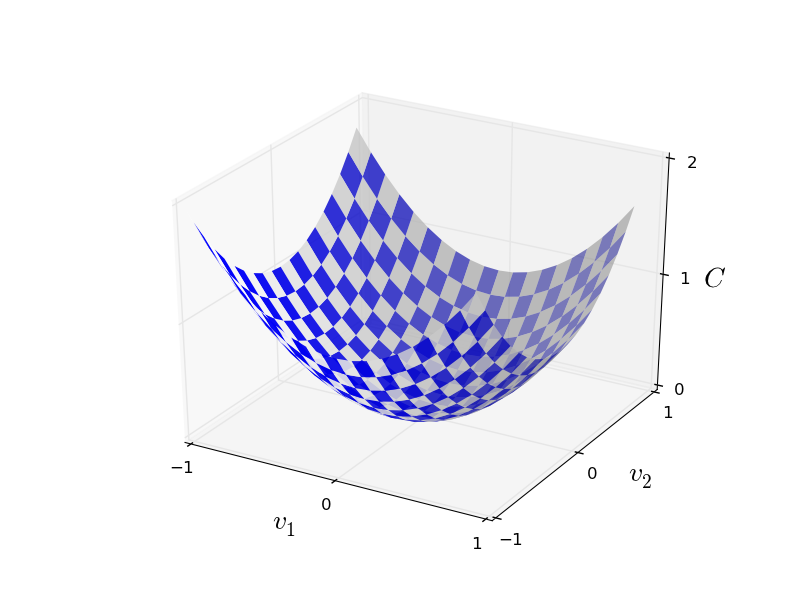
Մեր նպատակն է գտնել $C$-ի մինիմումի կետ(եր)ը: Իհարկե, եթե դիտարկենք վերևում պատկերված ֆունկցիայի գրաֆիկը, ապա կարող ենք տեսնել մինիմումի կետը: Սակայն դա բավականին պարզ ֆունկցիա է, համեմատած իրականության մեջ հանդիպող $C$-ի ավելի բարդ կառուցվածքներին (մեկից ավել փոփոխականի ֆունկցիաներ, որոնց գրաֆիկից ակնհայտ չեն մինիմումի կետերը):
Այկընտրանքային մոտեցում է, օգտագործելով մաթեմատիկական անալիզի գործիքները, անալիտիկորեն գտնել մինիմումը։ Կարող ենք հաշվել ածանցյալները և փորձել գտնել $C$-ի էքստրեմումի կետերը: Սա հնարավոր է, որ աշխատի, եթե $C$-ն մեկ կամ երկու փոփոխականների ֆունկցիա է, սակայն խնդիրը էապես կբարդանա, եթե մենք ունենանք շատ ավելի մեծ քանակությամբ փոփոխականներ: Նեյրոնային ցանցերի համար հատկապես փոփոխականների քանակը շատ ավելի շատ է: Մեծ ցանցերում արժեքի ֆունկցիաները կարող են կաված լինել միլլիոնավոր կշիռներից և շեղումներից (ընդ որում, լիելով բավականին բարդ կառուցվածքով ֆունկցիա): Այսպիսով, օգտագործելով մաթեմատիկական անալիզը, պրակտիկորեն հնարավոր չէ անալիտիկորեն գտնել մինիմումի կետերը:
Բարեբախտաբար, հայտնի է ալգորիթմ, որը օգտագործելով կարող ենք լուծել խնդիրը: Դիտարկենք հետևայլ անալոգիան: Մտածենք մեր ֆոունկցիայի մասին որպես հովիտ: Պատկերացնենք, որ գնդակը գլորվում է հովիտով դեպի ներքև: Ելնելով ամենօրյա մեր փոձից, կարող ենք ասել, որ գնդակը վերջիվերջո կհասնի հովիտի ստորոտին: Փոսձենք օգտագործել այս գաղափարը որպես մինիմումի կետը գտնելու մեթոդ: Մենք կընտրենք պատահական կետ որպես գնդակի սկզբնակետ և կսիմուլացնենք գնդակի ներքև գլորվելը ամեն քայլում որոշելով, թե որն է լինելու գնդակի գլորման ուղղությունը (կամ հաջորդ կետը, որով անցնելու է գնդակը): Դա կարող ենք իրականացնել հաշվելով $C$-ի ածանցյալները (երբեմն նաև երկրորդ կարգի): Այդ ածանցյալները մեզ ցույց կտան, թե ինչպիսի "տեսք" ունի հովիտը և, հետևաբար, թե ինչպես մեր գնդակը պետք է գլորվի:
Տպավորություն կարող է ստեղծվել, որ մենք սկսելու ենք օգտագործել Նյուտոնյան շարժման հավասարումները գնդակի համար` հաշվի առնելով գրավիտացիան, արագացումը և այլն: Իրականում գլորվող գնդակի անալոգիային այդպես լրջորեն չենք վերաբերվելու. մենք դուրս ենք բերում $C$-ի մինիմիզացնելու ալգորիթմ, այլ ոչ ֆիզիկայի օրենքների ճշգրիտ սիմուլյացիա: Գնդակի օրինակն ուղղակի նախատեսված է պատկերացում կազմելու համար, թե ինչ ալգորիթմ ենք պատրաստվում կառուցել: Այսպիսով, եթե մենք ունենայինք սուպեր կարողություններ և կարողանայինք պարտադրել սեփական ֆիզիկայի կանոնները` գնդակին թելադրելով, թե ինչպես այն պետք է շարժվի, ապա ի՞նչ օրենքներով կորոշեինք գնդակի շարժումն այնպես որ այն միշտ գլորվեր դեպի ստորոտը:
Որպեսզի ճշգրտենք այս հարցը, դիտարկենք, թե ինչ կպատահի, եթե գնդակը շարժենք $\Delta v_1$-ով $v_1$ ուղղությամբ և $\Delta v_2$-ով $v_2$-ի ուղղությամբ: Այսպիսով, $C$-ի փոփոխությունը կարելի է հաշվել հետևյալ բանաձևով. \begin{eqnarray} \Delta C \approx \frac{\partial C}{\partial v_1} \Delta v_1 + \frac{\partial C}{\partial v_2} \Delta v_2. \tag{7}\end{eqnarray} Եթե $\Delta C$-ն բացասական է, դա կնշանակի, որ $C$-ն նվազում է, այսինքն, ըստ մեր անալոգիայի, գնդակը գլորվում է դեպի ստորոտ: Հետևաբար, պետք է ընտրենք $\Delta v_1$-ի և $\Delta v_2$-ի այնպիսի արժեքներ, որպեսզի $C$-ն նվազի ամեն քայլից հետո: Փորձենք գտնել այդպիսի փոփոխություններ: Նշանակենք $\Delta v \equiv (\Delta v_1, \Delta v_2)^T$, որտեղ $T$-ն տրանսպոնացման գործողությունն է: Նշանակենք որպես $C$-ի գրադիենտ մասնակի ածանցյալների վեկտորը` $\left(\frac{\partial C}{\partial v_1}, \frac{\partial C}{\partial v_2}\right)^T$. Նշանակենք գրադիենտային վեկտորը հունական նաբլա տառով` $\nabla C$. \begin{eqnarray} \nabla C \equiv \left( \frac{\partial C}{\partial v_1}, \frac{\partial C}{\partial v_2} \right)^T. \tag{8}\end{eqnarray} Հարկ է նշել, որ $\nabla C$-ի նշանակման մեկնաբանությունը ոչ միանշանակ է: Այն կարելի է դիտարկել որպես մաթեմատիկական օբյեկտ կախված երկու մասից, որոնցից $\nabla$-ն ուղղակի նշանակում է, որ գրվածը գրադիենտ վեկտոր է: Սակայն կարելի է $\nabla$-ն դիտարկել որպես անկախ մաթեմատիկական ոբյեկտ, որտեղ այն հանդես է գալիս, օիրնակ որպես դիֆերենցման օպերատոր: Պայմանավորվենք դիտարկել $\nabla C$-ն առաջին նկարագրված (ավելի պարզեցված) ձևով:
Արտագրենք (7) արտահայտությունը որպես \begin{eqnarray} \Delta C \approx \nabla C \cdot \Delta v. \tag{9}\end{eqnarray} Այս հավասարումն օգնում է բացատրել, թե ինչու է $\nabla C$-ն կոչվում գրադիենտ: Այն ցույց է տալիս, թե ինչպես է $C$-ի փոփոխությունը կախված $v$-ի փոփոխությունից: Հետևաբար, այն հնարավորություն է տալիս $\Delta v$-ն այնպես ընտրել, որ $\Delta C$-ն ստանա բացասական արժեք: Ենթադրենք, որ ընտրում ենք \begin{eqnarray} \Delta v = -\eta \nabla C, \tag{10}\end{eqnarray} որտեղ $\eta$-ն բավականաչափ փոքր դրական թիվ է (հայտնի որպես ուսուցման գործակից (learning rate)). Հավասարում (9)-ը ցույց է տալիս, որ $\Delta C \approx -\eta \nabla C \cdot \nabla C = -\eta \|\nabla C\|^2$. Քանի որ $\| \nabla C \|^2 \geq 0$, ապա $\Delta C \leq 0$, հետևաբար $C$-ն միշտ կնվազի, եթե $v$-ն ընտրենք հաշվի առնելով հավասարում (10)-ը . (Իհարկե, այնպես, որ չխախտվի մոտավոր հավասարում (9)-ը ). Սա ըստ էության այն է, ինչ մենք փնտրում էինք, հետևաբար, մենք կվերցնենք հավասարում (10)-ը որպես «շարժման հավասարում» գնդակի համար: Դա էլ ըստ էության հիմքն է գրադիենտային իջեցման ալգորիթմ կառուցելու համար: Այսպիսով, օգտագործելով հավասարում (10)-ը և հաշվենք $\Delta v$-ի արժեքը, այնուհետև շարժենք գնդակը $v$ կետից $\Delta v$-ով. \begin{eqnarray} v \rightarrow v' = v -\eta \nabla C. \tag{11}\end{eqnarray} Այնուհետև կօգտագործենք այս օրենքը ևս մեկ անգամ, շարժելով գնդակը ևս մեկ քայլով: Շարունակելով այսպես, $C$-ն կնվազի այնքան մինչև ամենայն հավանականությամբ հասնի գլոբալ մինիմումին (կախված ֆունկցիայի հատկություններից իհարկե):
Ընդհանրացնելով, գրադիենտային վայրէջքի աշխատանքը կայանում է հետևյալում. հաշվել $\nabla C$ գրադիենտային վեկտորը, այնուհետև շարժվել հակառակ ուղղությամբ (գլորվելով դեպի հովիտի ստորոտը): Մենք կարող ենք դա պատկերել հետևյալ կերպ.
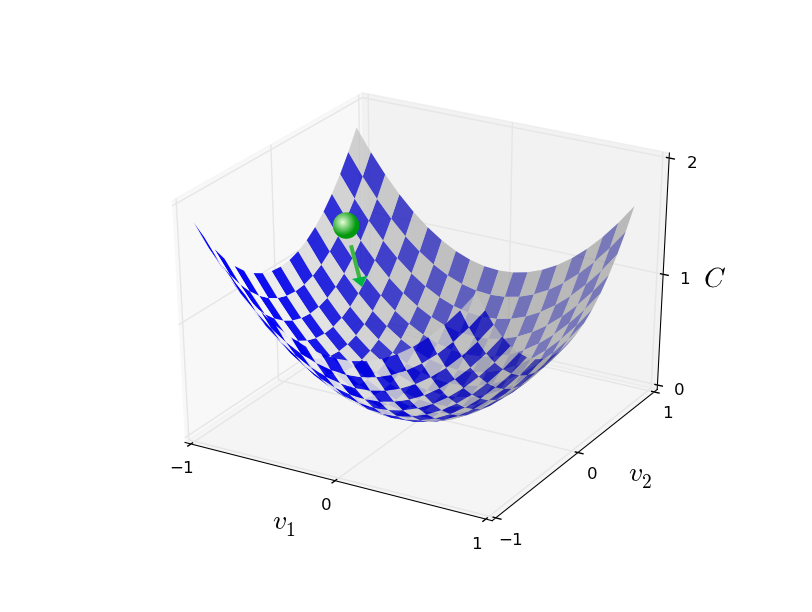
Որպեսզի գրադիենտային վայրէջքը ճիշտ աշխատի, պետք է $\eta$-ի արժեքը վերցնել բավարար չափով փոքր այնպես, որ (9) հավասարումը վերածվի լավ մոտարկման: Հակառակ դեպքում կարող ենք ստանալ $\Delta C > 0$, ինչը հակասում է մեր նպատակներին: Միևնույն ժամանակ, եթե $\eta$-ի արժեքը լինի շատ փոքր, ապա $\Delta v$-ի փոփոխությունները նույնպես կլինեն փոքր, հետևաբար գրադիենտային վայրէջքը կաշխատի դանդաղ: Ալգորիթմի պտակտիկ իրականացումներում, $\eta$-ի արժեքը փոխվում է այնպես, որ (9) հավասարումը լինում է լավ մոտարկում և ալգորիթմը շատ դանդաղ չի լինում: Հետագայում ավելի մանրամասն կտեսնենք, թե ինչպես է դա տեղի ունենում:
Մենք գրադիենտային վայրէջքին ծանոթացանք՝ ենթադրելով, որ $C$-ն երկու փոփոխականի ֆունկցիա է: Ըստ էության, ալգորիթմը աշխատում է ճիշտ նույն ձևով, անգամ եթե $C$-ն երկուսից ավելի փոփոխականների ֆունկցիա է: Ենթադրենք $C$-ն $v_1,\ldots,v_m$-ից կախված $m$ փոփոխականի ֆունկցիա է: Ապա $C$-ի $\Delta C$ փոփոխությունը, որն արդյունք է $\Delta v = (\Delta v_1, \ldots, \Delta v_m)^T$ փոփոխության, կարելի է արտահայտել հետևյալ հավասարումով. \begin{eqnarray} \Delta C \approx \nabla C \cdot \Delta v, \tag{12}\end{eqnarray} որտեղ $\nabla C$ գրադիենտը հետևյալ վեկտորն է. \begin{eqnarray} \nabla C \equiv \left(\frac{\partial C}{\partial v_1}, \ldots, \frac{\partial C}{\partial v_m}\right)^T. \tag{13}\end{eqnarray} Ինչպես երկու փոփոխականի դեպքում, կարող ենք որոշել \begin{eqnarray} \Delta v = -\eta \nabla C, \tag{14}\end{eqnarray} և (12) $\Delta C$-ի արտահայտությունը կլինի բացասական: Դա հնարավորություն է տալիս մեզ գրադիենտը ձգտեցնել մինիմումի պարբերաբար կիրառելով \begin{eqnarray} v \rightarrow v' = v-\eta \nabla C. \tag{15}\end{eqnarray} թարմացումը, անգամ եթե $C$-ն երկուսից ավել փոփոխականներից հավասարում է: Հենց այս թարմացման օրենքն էլ սահմանում է գրադիենտային վայրէջքի ալգորիթմը: Այն հնարավորություն է տալիս շարունակաբար փոխելով $v$-ի դիրքը գտնել $C$-ի մինիմում արժեք: Հարկ է նշել, որ այս փոփոխման օրենքը ոչ բոլոր դեպքերում է աշխատում: Բազմաթիվ իրավիճակներում գրադիենտային իջեցումը կարող է գլոբալ մինիմումի հայտնաբերման խնդրի լուծումը ձախողել (մենք այս հարցին կանդրադառնանք հետագա գլուխներում): Սակայն պարզվում է, որ հատկապես նեյրոնային ցանցերի դեպքում այն աշխատում է և արժեքի ֆունկցիան մինիմիզացնելու բավականին էֆեկտիվ մեթոդ է, այսպիսով օգնում է ցանցին մարզվել:
Տպավորություն է, որ գրադիենտային իջեցումը օպտիմալ մարտավարությունն է մինիմումը հայտնաբերելու համար: Ենթադրենք, որ փորձում ենք $\Delta v$ քայլ կատարել այնպես, որ $C$-ն նվազի հնարավորինս շատ: Սա համարժեք է $\Delta C \approx \nabla C \cdot \Delta v$ մինիմիզացնելուն: Սահմանափակենք քայլի չափն այնպես, որ $\| \Delta v \| = \epsilon$, որտեղ $\epsilon > 0$ և ֆիքսված է: Այլ կերպ ասած, մեզ պետք է փոքր հաստատուն քայլ, և փորձում ենք գտնել քայլի այնպիսի ուղղություն, որը $C$-ն կնվազեցնի հնարավորինս շատ: Կարելի է ապացուցել, որ $\nabla C \cdot \Delta v$-ն մինիմիզացնելու համար $\Delta v$-ի ընտրությունը կարելի է որոշել $\Delta v = - \eta \nabla C$ արտահայտությամբ, որտեղ $\eta = \epsilon / \|\nabla C\|$ որոշվում է $\|\Delta v\| = \epsilon$ սահմանափակման միջոցով: Այսպիսով, գրադիենտային վայրէջքը կարելի է դիտարկել որպես փոքր քայլեր անելու մարտավարություն այնպես, որ $C$-ն հնարավորինս նվազի:
Վարժություններ
- Ապացուցել վերջին պարբերության պնդումը: Հուշում. Եթե դեռ ծանոթ չեք
Կոշի-Շվարցի
անհավասարությանը, ապա ծանոթանալը կարող է օգնել այս խնդրի լուծմանը:
- Մենք դիտարկեցինք գրադիենտային վայրէջքը, երբ $C$-ն երկու կամ ավել փոփոխականների ֆունկցիա է: Ի՞նչ է տեղի ունենում, երբ $C$-ն մեկ փոփոխականի ֆունկցիա է: Կարո՞ղ եք բերել գրադիենտային իջեցման երկրաչափական մեկնաբանությունը միաչափ դեպքում:
Գրադիենտային վայրէջքի բազմաթիվ տարբերակներ են հետազոտվել մինչ այժմ` ներառելով այնպիսինները, որոնք հիմնված են գնդակի շարժումը կրկնօրինակելու վրա: Վերջիններս ունեն որոշակի առավելություններ, ինչպես նաև էական խնդիրներ. պարզվում է, որ պարտադիր է հաշվել $C$-ի երկրորդ կարգի ածանցյալները, ինչը ալգորոթմական տեսանկյունից էապես "թանկ" գործողություն է: Որպեսզի համոզվենք դրանում, ենթադրենք մեր նպատակն է հաշվել բոլոր երկրորդ կարգի ածանցյալները` $\partial^2 C/ \partial v_j \partial v_k$: Եթե $v_j$ փոփոխականների քանակը մեկ միլիոն է, ապա կարիք կլիներ հաշվել մոտավորապես տրիլիոն հատ երկրորդ կարգի մասնակի ածանցյալներ*։ *Իրականում մոտավորապես կես տրիլիոն, քանի որ $\partial^2 C/ \partial v_j \partial v_k = \partial^2 C/ \partial v_k \partial v_j$. Սակայն պարզ է, թե ինչի մասին է խոսքը: Դա հաշվարկման տեսանկյունից էապես «թանկ» գործողությունների համալիր է: Հաշվի առնելով վերը նշվածը` գոյություն ունեն հնարքներ նմանատիպ խնդիրները շրջանցելու համար, ընդ որում, գրադիենտային իջեցման ալտերնատիվների որոնումը ակտիվ ուսումնասիրության ուղղություն է: Այնուամենայնիվ, այս գրքում մենք կօգտագործենք գրադիենտային վայրէջքը որպես հիմնական միջոց՝ նեյրոնային ցանցերի միջոցով ուսուցումը կազմակերպելու համար:
Ինչպե՞ս կարող ենք օգտագործել գրադիենտային վայրէջքը նեյրոնային ցանցերով ուսուցման համար: Գաղափարը կայանում է նրանում, որ գրադիենտային վայրէջքը օգտագործենք $w_k$ կշիռները և $b_l$ շեղումները գտնելու համար, որոնք կմինիմիզացնեն գնի (6) ֆունկցիան: Որպեսզի տեսնենք, թե ինչպես է այն աշխատում, արտագրենք գրադիենտային վայրէջքի թարմացման օրենքը` $v_j$ փոփոխականները փոխարինելով կշիռներով և շեղումներով: Այսպիսով, գրադիենտային վայրէջքի թարմացման կանոնը կունենա հետևյալ տեսքը. \begin{eqnarray} w_k & \rightarrow & w_k' = w_k-\eta \frac{\partial C}{\partial w_k} \tag{16}\\ b_l & \rightarrow & b_l' = b_l-\eta \frac{\partial C}{\partial b_l}. \tag{17}\end{eqnarray} Շարունակաբար իրացնելով այս թարմացման օրենքը, մենք «կգլորվենք բլուրից ներքև» և ամենայն հավանականությամբ կգտնենք գնի ֆունկցիայի մինիմումը: Այլ կերպ ասած, սա այն օրենքն է, որի միջոցով նեյրոնային ցանցերը կմարզվեն:
Գրադիենտային իջեցման կիրառման հետ կապված կան որոշակի բարդություններ: Մենք դրանք խորությամբ կդիտարկենք ապագա գլուխներում: Այժմ դիտարկենք դրանցից մեկը միայն, որի համար դիտարկենք քառակուսային գնի հավասարումը (6) : Նկատենք, որ գնի ֆունկցիան ունի $C = \frac{1}{n} \sum_x C_x$ տեսքը, հետևաբար, այն առանձին մուտքային տվյալների համար $C_x \equiv \frac{\|y(x)-a\|^2}{2}$ արժեքների հանրահաշվական միջինն է: Պրակտիկորեն, որպեսզի հաշվարկենք $\nabla C$ գրադիենտը, մենք պետք է հաշվարկենք $\nabla C_x$ առանձին ամեն $x$ մուտքային տվյալի համար, այնուհետև հաշվենք նրանց $\nabla C = \frac{1}{n} \sum_x \nabla C_x$ հանրահաշվական միջինը: Դժբախտաբար շատ մեծ քանակությամբ ուսուցման տվյալների դեպքում սա կարող է բավական շատ ժամանակ տևել, հետևաբար ուսուցումը կարող է դանդաղել:
Ուսուցումն արագացնելու նպատակով կարելի է օգտագործել մի գաղափար, որը կոչվում է ստոկաստիկ գրադիենտային վայրէջք (stochastic gradient descent): Գաղափարը կայանում է նրանում, որ պետք է $\nabla C$ գրադիենտը գնահատել` հաշվելով ուսուցման տվյալներից փոքրիկ մասի $\nabla C_x$ գրադիենտները: Պարզվում է, որ միջինացնելով այդ փոքր հատվածի գրադիենտները՝, մենք արագորեն կարող ենք ստանալ իսկական $\nabla C$ գրադիենտի լավ գնահատական: Դա օգնում է գրադիենտային վայրէջքի, հետևաբար նաև մարզման արագացման հարցում։
Այսպիսով, ստոկաստիկ գրադիենտային վայրէջքը աշխատում է` պատահականորեն ընտրելով որոշակի ոչ մեծ քանակությամբ $m$ մարզման մուտքային տվյալներ: Այդ տվյալները նշանակենք որպես $X_1, X_2, \ldots, X_m$ և պայմանավորվենք հղվել նրանց որպես մինի-փաթեթ (mini-batch): Եթե $m$-ը բավականաչափ մեծ է, սպասվում է, որ $\nabla C_{X_j}$-ի հանրահաշվական միջինը մոտ կլինի $\nabla C_x$ հանրահաշվական միջինին: Այսպիսով, \begin{eqnarray} \frac{\sum_{j=1}^m \nabla C_{X_{j}}}{m} \approx \frac{\sum_x \nabla C_x}{n} = \nabla C, \tag{18}\end{eqnarray} որտեղ երկրորդ գումարը ամբողջ մարզման տվյալների երկայնքով է: Փոխելով հավասարման կողմերը, կստանանք \begin{eqnarray} \nabla C \approx \frac{1}{m} \sum_{j=1}^m \nabla C_{X_{j}}, \tag{19}\end{eqnarray} միևնույն ժամանակ համոզվելով, որ մենք կարող ենք գնահատել ամբողջ գրադիենտը միայն հաշվելով պատահականորեն ընտրված մինի-փաթեթի գրադիենտները:
Որպեսզի սա ուղղակիորեն կապենք նեյրոնային ցանցերով ուսուցման հետ, ենթադրենք, որ $w_k$ և $b_l$-ով նշանակված են մեր ցանցի կշիռներն ու շեղումները: Ապա, ստոկաստիկ գրադիենատային վայրէջքը աշխատում է պատահականորեն ընտրված մարզման մինի-փաթեթի տվյալների հիման վրա` \begin{eqnarray} w_k & \rightarrow & w_k' = w_k-\frac{\eta}{m} \sum_j \frac{\partial C_{X_j}}{\partial w_k} \tag{20}\\ b_l & \rightarrow & b_l' = b_l-\frac{\eta}{m} \sum_j \frac{\partial C_{X_j}}{\partial b_l}, \tag{21}\end{eqnarray} որտեղ գումարը մինի-փաթեթի բոլոր $X_j$ մարզման օրինակների երկայնքով է: Այնուհետև ընտրում ենք ուրիշ պատահականորեն ընտրված մինի-փաթեթ և կատարում ուսուցումը դրանց հիման վրա: Սա կատարում ենք այնքան ժամանակ, մինչև օգտագործած լինենք բոլոր մարզման մուտքային տվյալները: Այս պրոցեսը այլ կերպ կոչվում է մարզման դարաշրջան (epoch): Երբ ավարտում ենք ներկա մարզման դարաշրջանը, սկսում ենք նորն իրականացնել:
Հարկ է նշել, որ գնի ֆունկցիայի և կշռի ու շեղումների մինի-փաթեթային թարմացումների տարատեսակ մաշտաբավորումներ (scaling) են ընդունված: Դիտարկենք (6) հավասարումը, որտեղ արժեքի ֆունկցիան մաշտաբավորված է $\frac{1}{n}$-ով: Մարդիկ երբեմն բաց են թողնում $\frac{1}{n}$-ը, գումարելով արանձին մարզման օրինակների գնի ֆունկցիաները միջինացնելու փոխարեն: Սա կարող է օգտակար լինել, եթե մարզման օրինակների բազմությունը նախապես հայտնի չէ (օրինակ, երբ իրական ժամանակում տվյալ է գեներացվում): Նույն կերպ մինի-փաթեթի (20) և (21) թարմացման կանոնները երբեմն բաց են թողնում $\frac{1}{m}$ գործակիցը գումարի դիմացից: Կոնցեպտուալ առումով, սա էական փոփոխություն չի մտցնում, քանի որ այն համարժեք է ուսուցման գործակցի վերամաշտաբավորմանը (rescaling): Սակայն չարժե «ուշադրությունը թուլացնել այս թեմայի շուրջ»:
Մենք կարող ենք ստոկաստիկ գրադիենտային վայրէջքի մասին մտածել, որպես քաղաքական ցուցակագրում. շատ ավելի հեշտ է օգտագործել փոքր մինի-փաթեթ, քան կիրառել գրադիենտային վայրէջքը ամբողջ փաթեթի վրա, ինչպես, օրինակ, շատ ավելի հեշտ է կատարել քաղաքական հարցում բնակչության մի հատվածի վրա, քան իտականացնել ընտրություններ: Օրինակ, եթե ունենք $n = 60,000$ ուսուցման տվյալներ, ինչպես MNIST-ում է, և ընտրենք որպես մինի-փաթեթի երկարություն $m = 10$, ապա կունենանք գրադիենտի մոտարկման արագության $6,000$ անգամ լավացում: Իհարկե մոտարկումը կատարյալ չի լինի, կլինեն ստատիստիկ տատանումներ, բայց կարիք չկա, որպեսզի այն կատարյալ լինի: Մեզ միայն հետաքրքրում է շարժվել այն ուղղությամբ, որը կնվազեցնի $C$-ն: Դա նշանակում է, որ գրադիենտի ավելորդ հաշվարկման կարիք չունենք։ Պրակտիկորեն, ստոկաստիկ գրադիենտային վայրէջքը հաճախակի օգտագործվող և զորեղ մոտեցում է նեյրոնային ցանցերի մարզման համար և մարզման բազմաթիվ հմտությունների հիմքում է, որոնցից շատերը կդիրարկենք այս գրքում:
Վարժություն
- 1 մինի փաթեթով գրադիենտային իջեցումը գրադիենտային վայրէջքի ծայրահեղ տարբերակ է: Այսպիսով, տրված է $x$ ուսուցման մուտքը, կշիռներն ու շեղումները թարմացվում են $w_k \rightarrow w_k' = w_k - \eta \partial C_x / \partial w_k$ and $b_l \rightarrow b_l' = b_l - \eta \partial C_x / \partial b_l$ օրենքի համաձայն: Այնուհետև ընտրում ենք ևս մեկ մուտք և թարմացնում կշիռներն ու շեղումները ևս մեկ անգամ և այսպես շարունակ: Այս պրոցեսը հայտնի է որպես առցանց (online) կամ աճող (incremental) ուսուցում: Առցանց ուսուցման ընթացքում նեյրոնային ցանցը սովորում է` ամեն պահի օգտագործելով ճիշտ մեկ մարզման տվյալ (այնպես ինչպես մարդիկ են սովորում): Նշեք առցանց ուսուցման մեկ առավելությու և մեկ թերություն համեմատած ստոկաստիկ գրադիենտային ուսուցման հետ, որն օգտագործում է ասենք $20$ չափանի մինի փաթեթ:
Սահմանափակենք այս հատվածը քննարկելով մի հարց ևս, որը երբեմն շփոթեցնում է մարդկանց, ովքեր նոր են ծանոթանում գրադիենտային վայրէջքին: Նեյրոնային ցանցերում $C$-ն գնի ֆունկցիա է բազմաթիվ փոփոխականներից (բոլոր կշիռներն ու շեղումները) և սահմանում է հարթություն բազմաչափ տարածության մեջ: Որոշ մարդիկ սկսում են անհանգստանալ այն մասին, որ պետք է պատկերել բոլոր այդ տարածությունները, որի խնդիրը կայանում է նրանում, որ շատերը կարծում են, որ իրենք չեն կարող պատկերել կամ պատկերացնել 3-ից ավել տարածություններ: Գոյություն ունի՞ այնպիսի մի հատուկ կարողություն, որ այդ մարդիկ բաց են թողնում, այնպիսի կարողություն, որ իրական սուպեր մաթեմատիկոսները ունեն: Իհարկե պատասխանն է ոչ: Անգամ ամենից արհեստավարժ մաթեմատիկոսները չեն կարող պատկերել 4 չափանի տարածությունները հասկանալի ձևով: Փոխարենը նրանք օգտագործում են ներկայացման այլընտրանքային միջոցներ կառուցելու հնարքներ: Դա այն է, ինչ մենք արեցինք վերևում. մենք տեսողականի փոխարեն օգտագործեցինք $\Delta C$ ներկայացնելու հանրահաշվական տեսքը, որպեսզի հասկանանք, թե ինչպես նվազեցնենք $C$-ն: Մարդիկ, ովքեր կարողանում են էֆֆեկտիվ մտածել բազմաչափ տարածություններում, ունեն այլ տարբեր հնարքների մտավոր գրադարան. մեր հանրահաշվական միջոցը միայն մեկ օրինակ է: Այդպիսի հնարքներ կարելի է սովորել, չնայած նրանցից շատերը չունեն եռաչափ տարածություն պատկերելու պարզությունները: Այս թեմայով հետաքրքրվողներին հրավիրում ենք ընթերցել հետևյալ զրույցը այն բանի մասին, թե ինչպես են մատեմատիկոսներն օգտագործում որոշ հնարքներ բազմաչափ տարածություններում մտածելու համար: Կարող է քննարկված հնարքներից որոշները բավականին բարդ լինեն, սակայն մեծ մասը ինտուտիվ են և հասանելի, այնպես որ կամայական մարդ կարող է տիրապետել բավարար ջանք գործադրելուց հետո:
Թվանշանները ճանաչող ցանցի իրականացումը
Առաջարկում եմ կառուցել ծրագիր, որը սովորում է, թե ինչպես ճանաչել ձեռագիր թվանշանները` օգտագործելով ստոկաստիկ գրադիենտային վայրէջքը և MNIST ուսուցման տվյալների բազմությունը: Որպես առաջին գործողություն փորձենք MNIST տվյալները զետեղել համակարգչում: Եթե դուք git տարբերակների կառավարման (version control) գործիքի օգտտեր եք, ապա կարող եք ձեռք բերել տվյալները՝ կլոնավորելով սույն գրքի կոդի շտեմարանից,
git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git
Եթե դուք չեք օգտագործում git, ապա կարող եք ներբեռնել տվյալներն ու կոդը այստեղից
Ի դեպ, երբ ավելի վաղ նկարագրում էինք MNIST տվյալները, նշեցինք, որ այն բաժանված է 60,000 ուսուցման և 10,000 թեստավորման նկարների: Դա պաշտոնական նկարագրությունն է: Իրականում, մենք պատրաստվում ենք տվյալները բաժանել այլ կերպ: Առաջարկում եմ թողնել թեստավորման նկարները նույնը, սակայն բաժանել MNIST-ի 60,000 մարզման նկարները երկու մասի. նկարների 50,000-անոց բազմություն, որը կօգտագործենք որպես մարզման տվյալներ և նկարների 10,000-անոց բազմություն, որը կօգտագործենք որպես վավերացման բազմություն (validation set): Այս գլխում վավերացման բազմությունը չենք օգտագործի, սակայն ավելի ուշ կօգտագործենք այն, որպեսզի որոշենք նեյրոնային ցանցերի հիպեր պարամետրերը (hyper-parameters)` ուսուցման գործակիցը (learning rate) և այլն: Չնայած նրան, որ վավերացման տվյալները օրիգինալ MNIST սպեցիֆիկացիայի մաս չեն, շատերն օգտագործում են MNIST-ն այդ կերպ և վավերացման տվյալների օգտագործումը տարածված պրակտիկա է նեյրոնային ցանցերում: Այսպիսով, այսուհետ, երբ հղում կատարենք MNIST մարզման տվյալներին, ապա դա կնշանակի հղում 50,000 տվյալներին* *Ինչպես ավելի վաղ նշվել էր, MNIST տվյալների բազմությունը հիմնված NIST-ի (United States' National Institute of Standards and Technology) կողմից հավաքագրված երկու տվյալների բազմությունների հիման վրա: MNIST կառուցելու համար, NIST-ի տվյալները Յանն Լեքունի, Կորինա Կորտեսի և Քրիստոֆեր Ջեյ ՍԻ Բուրգեսի կողմից ենթարկվել են ֆորմատի փոփոխության` տվյալների հետ աշխատանքն ավելի հարմարավետ դարձնելու նպատակով: Մանրանասների համար, այցելեք այս հղումով: Այս գրքի կոդի շտեմարանում տվյալներն այնպիսի տեսքով են, որը հեշտացնում է բեռնումն ու Python-ի միջոցով մանիպուլյացիաների իրականացումը: Ես ձեռք եմ բերել այս տվյալների այսպիսի տեսքը Մոնրեալի Համալսարանի LISA մեքենայական ուսուցման լաբարատորիայից link):
MNIST տվյալներից բացի մեզ պետք է նաև Python-ի Numpy կոչվող գրադարանը, որպեսզի իրականացնենք գծային հանրահաշվի խնդիրները: Գրադարանը կարող եք տեղադրել այստեղից:
Թույլ տվեք, մինչ ամբողջական ներկայացնելը, նկարագրել նեյրոնային ցանցերի կոդի հիմնական մասերը: Կարևորագույն կտորը դա Network դասն է, որը ներկայացնում է նեյրոնային ցանցը: Ահա Network օբյեկտի կոնստրուկտորը:
class Network(object):
def __init__(self, sizes):
self.num_layers = len(sizes)
self.sizes = sizes
self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(sizes[:-1], sizes[1:])]
Այս կոդում sizes ցուցակը պարունակում է համապատասխան շերտերում նեյրոնների քանակը: Օրինակ, երբ ցանկանում ենք ստեղծել Network օբյեկտ, որի առաջին շերտը կազմված է 2 նեյրոններից, երկրորդ շերտը կազմված է 3 նեյրոններից և վերջին երրորդ շերտը կազմված է 1 նեյրոնից, ապա կարող ենք դա իրականացնել հետևյալ կոդի միջոցով.
net = Network([2, 3, 1])
Նկատենք նաև, որ շեղումներն ու կշիռները պահվում են որպես Numpy մատրիցներ: Օրինակ, net.weights[1]-ը Numpy մատրից է, որում պահվում են երկրորդ և երրորդ շերտերն իրար կապող կշիռները (այլ ոչ առաջին և երկրորդ շերտերը, քանզի Python-ի ցուցակների ինդեքսավորումը սկսվում է 0-ից): Քանի որ net.weights[1] երկար է գրվում, ապա պարզապես նշանակենք այն $w$-ով: Այն այնպիսի մատրից է, որի $w_{jk}$ անդամը ցույց է տալիս երկրորդ շերտի $k^{\rm րդ}$ և երրորդ շերտի $j^{\rm րդ}$ նեյրոններին կապող կշիռը: թվում է, թե $j$ և $k$ ինդեքսների հերթականությունն ավելի ինտուիտիվ կլիներ, եթե դիրքերով շրջված լինեին, սակայն այդպիսի հերթականության առավելությունը կայանում է նրանում, որ երրորդ շերտի ելքային արժեքների վեկտորը կարող ենք գրել որպես \begin{eqnarray} a' = \sigma(w a + b). \tag{22}\end{eqnarray} Փորձենք բացատրել այս հավասարման կառուցվածքը: $a$-ն նեյրոնների երկրորդ շերտի ելքային արժեքների(ակտիվացիաների) վեկտորն է: $a'$-ը ստանալու համար $a$-ն բազմակատկվում է $w$ մատրիցով, որին ավելացվում է $b$ շեղումների վեկտորը: Այնուհետև $\sigma$-ն կիրառում ենք էլեմենտ առ էլեմենտ $w a +b$ վեկտորի վրա (նշենք, որ ֆունկցիայի էլեմենտ առ էլեմենտ կիրառումը վեկտորի վրա կոչվում է ֆունկցիայի վեկտորացում): Հեշտ է համոզվել, որ (22) հավասարումը տալիս է նույն արժեքը, ինչ ավելի վաղ մեր դուրս բերած (4) հավասարումը, որը հաշվում է սիգմոիդ նեյրոնի ելքային արժեքը:
Վարժություն
- Ցույց տվեք, որ (22) հավասարումը նույն արդյունքն է տալիս, ինչ rule (4) արտահայտությունը սիգմոիդ նեյրոնների ելքային արժեքի հաշվման համար:
Հաշվի առնելով այս ամենը, դյուրին է կառուցել Network-ի ելքային արժեքը հաշվող ծրագրի իրականացումը: Սկսենք սիգմոիդի ֆունկցիայի սահմանումից.
def sigmoid(z):
return 1.0/(1.0+np.exp(-z))
Այնուհետև ավելացնենք Network դասի feedforward մեթոդը, որը տրված ցանցի a մուտքային պարամետրի դեպքում վերադարձնում է համապաասխան արժեքը * ** Ենթադրվում է, որ a մուտքային պարամետրը (n, 1) միջակայքում գտնվող Numpy ndarray է, այլ ոչ (n,) չափանի վեկտոր: Այստեղ n-ը ցանցի մուտքային վեկտորի երկարությունն է: Եթե փորձեք (n,) վեկտորն օտգագործել որպես մուտքային արժեք, ապա կստացվեն տարօրինակ արդյունքներ: Չնայած նրան, որ (n,) վեկտորի օգտագործումը ավելի բնական ընտրություն է թվում, (n, 1) չափանի ndarray-ի օգտագործումը բավականին հեշտացնում է կոդի այնպիսի փոփոխությունները, որի արդյունքում կարող ենք միաժամանակ մեկից ավելի մուտքային արժեքներով կատարենք մարզումը, որը երբեմն հարմարավետ է: : Մեթոդը պարզապես կիրառում է (22) հավասարումը շերտ առ շերտ.
def feedforward(self, a):
"""Return the output of the network if "a" is input."""
for b, w in zip(self.biases, self.weights):
a = sigmoid(np.dot(w, a)+b)
return a
Իհարկե, մեր հիմնական նպատակն է Network օբյեկտների ուսուցումը: Այդ իսկ պատճառով իրականացնենք SGD ստոկաստիկ գրադիենտային վայրէջքի ալգորիթմը: Ահա իրականացումը: Այն կարող է առաջին հայացքից փոքր ինչ «խորհրդավոր» թվալ տեղ-տեղ, սակայն մենք ավելի ուշ այն մանրամասն կդիտարկենք:
def SGD(self, training_data, epochs, mini_batch_size, eta,
test_data=None):
"""Train the neural network using mini-batch stochastic
gradient descent. The "training_data" is a list of tuples
"(x, y)" representing the training inputs and the desired
outputs. The other non-optional parameters are
self-explanatory. If "test_data" is provided then the
network will be evaluated against the test data after each
epoch, and partial progress printed out. This is useful for
tracking progress, but slows things down substantially."""
if test_data: n_test = len(test_data)
n = len(training_data)
for j in xrange(epochs):
random.shuffle(training_data)
mini_batches = [
training_data[k:k+mini_batch_size]
for k in xrange(0, n, mini_batch_size)]
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta)
if test_data:
print "Epoch {0}: {1} / {2}".format(
j, self.evaluate(test_data), n_test)
else:
print "Epoch {0} complete".format(j)
training_data-ն (x, y) զույգերի ցուցակ է, որը ներկայացնում է մարզման մուտքային տվյալները և համապատասխան ցանկալի ելքային արժեքները: epochs և mini_batch_size փոփոխականները ներկայացնում են մարզման դարաշրջանների քանակը և մինի-փաթեթների չափը տվյալների նմուշագրման (sampling) ժամանակ: eta-ն $\eta$ ուսուցման գործակիցն է: Եթե test_data տրված է, ապա ծրագիրը կգնահատի ցանցը յուրաքանչյուր մարզման դարաշրջանից հետո և կարտատպի մասնակի առաջխաղացումները: Այն օգտակար է, որպեսզի հետևենք ծրագրի պրոգրեսին, սակայն դա մյուս կոմից կարող է էապես դանդաղեցնել ծրագիրը:
Կոդն աշխատում է հետևյալ կերպ: Յուրաքանչյուր դարաշրջանում այն սկսում է մարզման տվյալները պատահական խառնելուց այնուհետև բաժանում է համապատասխան երկարության մինի-փաթեթների: Դա մարզման տվյալների պատահական մնուշագրման հեշտ ձև է: Այնուհետև յուրաքանչյուր mini_batch-ի համար կիրառում ենք գրադիենտային վայրէջքի մեկ քայլ: Դա կատարվում է self.update_mini_batch(mini_batch, eta) կոդի միջոցով, որը ցանցի կշիռներն ու շեղումները թարմացնում է գրադիենտային իջեցման մեկ իտերացիայի հիման վրա՝ օգտագործելով միայն mini_batch-ում գտնվող մարզման տվյալները: Ահա update_mini_batch մեթոդի կոդը.
def update_mini_batch(self, mini_batch, eta):
"""Update the network's weights and biases by applying
gradient descent using backpropagation to a single mini batch.
The "mini_batch" is a list of tuples "(x, y)", and "eta"
is the learning rate."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
self.backprop-ի կոդը դեռևս չենք դիտարկի: Մենք կսովորենք հետադարձ տարածման (backpropagation) աշխատանքը հաջորդ գլխում, այդ թվում նաև կդիտարկենք self.backprop-ի կոդը: Այժմ պարզապես ենթադրենք, որ այն աշխատում է վերը նշվածի համաձայն՝ վերադարձնելով x մարզման օրինակին համապատասխան գնի գրադիենտը:
Այժմ դիտարկենք ամբողջական ծրագիրը, այդ թվում նաև դոկումենտացիան, որը վերևում բաց էր թողնված: self.backprop-ից զատ, ծրագիրը ինքն իրեն նկարագրում է՝ self.SGD-ում և self.update_mini_batch -ում տեղի են ունենում հիմնական գործողությունները, որոնք արդեն քննարկել ենք: self.backprop-ն օգտագործում է մի քանի հավելյալ ֆունկցիաներ գրադիենտների հաշվման նպատակով ( sigmoid_prime-ը, որը հաշվում է $\sigma$ ֆունկցիայի ածանցյալը և self.cost_derivative-ը, որը հաշվում է գնի ածանցյալը): Այդ ֆունկցիաներն այստեղ չենք նկարագրի, քանի որ դրանք մանրամասն կդիտարկենք հաջորդ գլխում: Չնայած այն փաստին, որ ծրագիրը ֆիզիկապես երկար է, կոդի մեծ մասը կազմում են բացատրական մեկնաբանության համար գրված տողերը: Ամբողջական կոդը կարելի է գտնել GitHub-ում՝ այստեղ։
"""
network.py
~~~~~~~~~~
A module to implement the stochastic gradient descent learning
algorithm for a feedforward neural network. Gradients are calculated
using backpropagation. Note that I have focused on making the code
simple, easily readable, and easily modifiable. It is not optimized,
and omits many desirable features.
"""
#### Libraries
# Standard library
import random
# Third-party libraries
import numpy as np
class Network(object):
def __init__(self, sizes):
"""The list ``sizes`` contains the number of neurons in the
respective layers of the network. For example, if the list
was [2, 3, 1] then it would be a three-layer network, with the
first layer containing 2 neurons, the second layer 3 neurons,
and the third layer 1 neuron. The biases and weights for the
network are initialized randomly, using a Gaussian
distribution with mean 0, and variance 1. Note that the first
layer is assumed to be an input layer, and by convention we
won't set any biases for those neurons, since biases are only
ever used in computing the outputs from later layers."""
self.num_layers = len(sizes)
self.sizes = sizes
self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(sizes[:-1], sizes[1:])]
def feedforward(self, a):
"""Return the output of the network if ``a`` is input."""
for b, w in zip(self.biases, self.weights):
a = sigmoid(np.dot(w, a)+b)
return a
def SGD(self, training_data, epochs, mini_batch_size, eta,
test_data=None):
"""Train the neural network using mini-batch stochastic
gradient descent. The ``training_data`` is a list of tuples
``(x, y)`` representing the training inputs and the desired
outputs. The other non-optional parameters are
self-explanatory. If ``test_data`` is provided then the
network will be evaluated against the test data after each
epoch, and partial progress printed out. This is useful for
tracking progress, but slows things down substantially."""
if test_data: n_test = len(test_data)
n = len(training_data)
for j in xrange(epochs):
random.shuffle(training_data)
mini_batches = [
training_data[k:k+mini_batch_size]
for k in xrange(0, n, mini_batch_size)]
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta)
if test_data:
print "Epoch {0}: {1} / {2}".format(
j, self.evaluate(test_data), n_test)
else:
print "Epoch {0} complete".format(j)
def update_mini_batch(self, mini_batch, eta):
"""Update the network's weights and biases by applying
gradient descent using backpropagation to a single mini batch.
The ``mini_batch`` is a list of tuples ``(x, y)``, and ``eta``
is the learning rate."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]
def backprop(self, x, y):
"""Return a tuple ``(nabla_b, nabla_w)`` representing the
gradient for the cost function C_x. ``nabla_b`` and
``nabla_w`` are layer-by-layer lists of numpy arrays, similar
to ``self.biases`` and ``self.weights``."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# feedforward
activation = x
activations = [x] # list to store all the activations, layer by layer
zs = [] # list to store all the z vectors, layer by layer
for b, w in zip(self.biases, self.weights):
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid(z)
activations.append(activation)
# backward pass
delta = self.cost_derivative(activations[-1], y) * \
sigmoid_prime(zs[-1])
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
# Note that the variable l in the loop below is used a little
# differently to the notation in Chapter 2 of the book. Here,
# l = 1 means the last layer of neurons, l = 2 is the
# second-last layer, and so on. It's a renumbering of the
# scheme in the book, used here to take advantage of the fact
# that Python can use negative indices in lists.
for l in xrange(2, self.num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
return (nabla_b, nabla_w)
def evaluate(self, test_data):
"""Return the number of test inputs for which the neural
network outputs the correct result. Note that the neural
network's output is assumed to be the index of whichever
neuron in the final layer has the highest activation."""
test_results = [(np.argmax(self.feedforward(x)), y)
for (x, y) in test_data]
return sum(int(x == y) for (x, y) in test_results)
def cost_derivative(self, output_activations, y):
"""Return the vector of partial derivatives \partial C_x /
\partial a for the output activations."""
return (output_activations-y)
#### Miscellaneous functions
def sigmoid(z):
"""The sigmoid function."""
return 1.0/(1.0+np.exp(-z))
def sigmoid_prime(z):
"""Derivative of the sigmoid function."""
return sigmoid(z)*(1-sigmoid(z))
Ի՞նչ հաջողությամբ է ծրագիրը ճանաչում ձեռագիր թվանշանները: Սկսենք MNIST-ի տվյալները բեռնելուց: Մենք դա կանենք՝ օգտագործելով հետևյալ փոքրիկ օգնական ծրագիրը՝ mnist_loader.py, որը նկարագրված է ներքևում: Աշխատեցնենք հետևյալ հրամանները Python-ի վահանակում:
>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
Իհարկե, սա կարելի էր իրականացնել առանձին Python ծրագրում, սակայն ամենայն հավանականությամբ ամենադյուրինը Python-ի վահանակում այն իրականացնելն է:
MNIST-ի տվյալները բեռելուց հետո կստեղծենք Network $30$ թաքնված նեյրոններով։ Մենք դա անում ենք վերևում սահմանված network անունով ծրագիրը ներմուծելուց հետո.
>>> import network
>>> net = network.Network([784, 30, 10])
Վերջապես, կօգտագործենք ստոկաստիկ գրադիենտայի իջեցում, որպեսզի սովորենք MNIST-ից կառուցված training_data-ից 30 դարաշրջանների ընթացքում, որտեղ մինի-փաթեթի երկարությունն ընտրված է 10 և ուսուցման գործակիցը՝ $\eta = 3.0$
>>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
Նկատենք, որ եթե ծրագիրն աշխատեցնում եք գիրքը կարդալուն զուգընթաց, ապա այն մինչև վերջ աշխատացնելու վրա որոշ ժամանակ կպահանջվի: Ես առաջարկում եմ ծրագիրը միացնեք, որպեսզի այն աշխատի և շարունակեք կարդալը և ժամանակ առ ժամանակ ստուգեք կոդի տպած ելքերը տերմինալում: Եթե շտապում եք, ապա կարող եք աշխատանքն արագացնել դարաշրջանները նվազեցնելով, կամ նվազեցնելով թաքնված նեյրոնների քանակը կամ օգտագործելով միայն մարզման տվյալների մի մասը: Պետք է նշել, որ արտադրական (production) կոդն անհամեմատ ավելի արագ կաշխատեր. հետևյալ Python սկրիտպները նախատեսված են ոչ թե լինելու արտադրությունում աշխատող արագագործ ծրագրեր, այլ օգնելու ընթերցողին Նեյրոնային ցանցերի աշխատանքը հասկանալու համար: Եվ, իհարկե, նեյրոնային ցանցերը մարզելուց հետո այն բավականին արագագործ կլինի համարյա բոլոր պլատֆորմներում: Օրինակ, այն բանից հետո, երբ մենք ուսուցանենք կշիռների և շեղումների բավարար լավ գուշակող բազմություն, ապա այն կարող ենք տեղափոխել, օրինակ բրաուզերային միջավայր և աշխատացնել Javascript-ի միջոցով կամ իրականացնել նույնը որևիցէ մոբայլ պլատֆորմի վրա, որպես բնիկ (native) ծրագիր: Ահա որոշակի մաս նեյրոնային ցանցի մեկ մարզման աշխատանքից: հետևյալ տրանսկրիպտը ցույց է տալիս, թե քանի փորձնական նկար է ճանաչվել նեյրոնային ցանցի կողմից մարզման յուրաքանչյուր դարաշրջանից հետո: Ինչպես կարող եք տեսնել, միայն մեկ դարաշրջանից հետո այն հասել է 10,000-ից 9,129 ճշգրիտ ճանաչման և այդ թիվը շարունակում է աճել:
Epoch 0: 9129 / 10000
Epoch 1: 9295 / 10000
Epoch 2: 9348 / 10000
...
Epoch 27: 9528 / 10000
Epoch 28: 9542 / 10000
Epoch 29: 9534 / 10000
Այսպիսով, մարզված ցանցը տալիս է մոտավորապես $95$ տոկոս ճշտությամբ դասակարգում՝ $95.42$ լինելով ամենաբարձր դասակարգման ճշտության արժեքը ("Epoch 28")։ Դա բավականին ոգևորիչ է առաջին քայլի համար: Սակայն հաշվի առեք խնդրում եմ, որ երբ դուք աշխատեցնեք ծրագիրն, ապա ձեզ մոտ ստացված արժեքները կարող են տարբերվել ինձ մոտ ստացված արժեքներից քանի որ ցանցի սկզբնարժեքավորումն իրականացվում է պատահականության սկզբունքով, որի հետևանքով տարբեր արժեքներ կունենան կշիռներն ու շեղումները: Այս գլխում տեղ գտած արժեքները երեք փորձի արդյունքում ստացված արդյունքներից լավագույնն է:
Վերագործարկենք վերևում գրված ծրագիրը՝ թաքնված նեյրոնների քանակը դարձնելով $100$։ Ինչպես արդեն նշել էինք, եթե ծրագիրը գործարկում եք կարդալուն զուգընթաց, ապա հաշվի առեք, որ որոշակի ժամանակ կպահանջվի մինչև ծրագրի աշխատանքի վերջանալը (իմ մեքենայի վրա այս փորձարկումը տևում է տասնյակ վայրկյաններ յուրաքանչյուր մարզման դարաշրջանի համար), հետևաբար իմաստալից կլինի ծրագրի աշխատանքին զուգընթաց շարունակել կարդալը:
>>>
net
=
network
.
Network([784, 100, 10])
>>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
Իհարկե, սա արդյունքները բարելավում է $96.59$ տոկոսի: Գոնե այս դեպքում, ավել թաքնված նեյրոններ օգտագործելն օգնում է ստանալ բարելավված արդյունքներ * *Ընթերցողների հետադարձ կապը այս փորձարկման համար ցույց է տալիս արդյունքների տարբերություն և որոշ մարզումների արդյունքները ընդհուպ հուսադրող չեն։ Երրորդ գլխում ներկայացված տեխնիկաները էապես կնվազեցնեն կատարողականության տարբերությունները մեր ցանցի տարբեր մարզումներից հետո։ ։
Իհարկե, այս ճշգրտությունները ստանալիս, կատարվել է մարզման դարաշրջանների քանակի, մինի-փաթեթի չափի և $\eta$ մարզման գործակցի ընտրություններ: Ինչպես նշված է վերևում, այս պարամետրերը կոչվում են նեյրոնային ցանցի հիպերպարամետրեր, որպեզի տարբերենք իրենց ցանցի այն պարամետրերից(կշիռներ և շեղումներ), որոնք ուսուցանվում են մարզման ընթացքում: Եթե հիպերպարամետրերը հաջող չընտրենք, կարող է լավ արդյունքներ չստանանք։ Ենթադրենք, որ ուսուցման գործակիցն ընտրել ենք որպես $\eta = 0.001$
>>> net = network.Network([784, 100, 10])
>>> net.SGD(training_data, 30, 10, 0.001, test_data=test_data)
Արդյունքներն ավելի քիչ հուսադրող են.
Epoch 0: 1139 / 10000
Epoch 1: 1136 / 10000
Epoch 2: 1135 / 10000
...
Epoch 27: 2101 / 10000
Epoch 28: 2123 / 10000
Epoch 29: 2142 / 10000
Ընդհանուր առմամբ նեյրոնային ցանցերի վրիպազերծումը (debugging) կարող է դժվարություններ առաջացնել։ Դա հատկապես տեղի ունի, երբ հիպեր-պարամետրերի ընտրությունը հանգեցնում է պատահական աղմուկի (random noise)։ Ենթադրենք, որ մենք փորձում ենք 30 թաքնված նեյրոններով ցանցային հաջողված արխիտեկտուրա, որի ուսուցման գործակիցը $\eta = 100.0$ է։
>>> net = network.Network([784, 30, 10])
>>> net.SGD(training_data, 30, 10, 100.0, test_data=test_data)
Epoch 0: 1009 / 10000
Epoch 1: 1009 / 10000
Epoch 2: 1009 / 10000
Epoch 3: 1009 / 10000
...
Epoch 27: 982 / 10000
Epoch 28: 982 / 10000
Epoch 29: 982 / 10000
Այս ամենից հետևությունն այն է, որ նեյրոնային ցանցերի վրիպազերծումը տրիվիալ չէ և պահանջում է հատուկ մոտեցումներ, որոնք պետք է յուրացնել, եթե նպատակ ունեքլ նեյրոնային ցանցերից լավ արդյունքներ ստանա։ Ընդհանրապես, մեզ պետք են լավ հիպերպարամետրեր և կառուցվածք ընտրելու մոտեցումներ։ Այս թեմայով մենք կխոսենք ամբողջ գրքի ընթացքում, ներառյալ նաև, թե ինչպես ենք վերևի հիպերպարամետրերն ընտրելու։
Վարժություն
- փորձեք կառուցել երկշերտ ցանց միայն մուտքային և ելքային շերտերով՝ համատասխանաբար 784 և 10 նեյրոններով։ Մարզեք ցանցը ստոկաստիկ գրադիենտային վայրէջքի միջոցով։ Ինչպիսի՞ ճշտությամբ դասակարգում կարող եք ստանալ։
Նկատենք, որ մենք բաց ենք թողել MNIST տվյալների բեռնման մանրամասերը։ Ահա, տեսեք կոդը ներքևում. MNIST տվյալների պահման համար օգտագործվող տվյալների կառուցվածքները ներկայացված են մեկնաբանություններում։ Այն բավականին պարզ է՝ ցուցակներ և շարքեր արտահայտված Numpy ndarray օբյեկտների միջոցով (եթե ծանոթ չեք ndarray-ների հետ, ապա պատկերացրեք այդ տվյալների տիպերը որպես վեկտորներ).
"""
mnist_loader
~~~~~~~~~~~~
A library to load the MNIST image data. For details of the data
structures that are returned, see the doc strings for ``load_data``
and ``load_data_wrapper``. In practice, ``load_data_wrapper`` is the
function usually called by our neural network code.
"""
#### Libraries
# Standard library
import cPickle
import gzip
# Third-party libraries
import numpy as np
def load_data():
"""Return the MNIST data as a tuple containing the training data,
the validation data, and the test data.
The ``training_data`` is returned as a tuple with two entries.
The first entry contains the actual training images. This is a
numpy ndarray with 50,000 entries. Each entry is, in turn, a
numpy ndarray with 784 values, representing the 28 * 28 = 784
pixels in a single MNIST image.
The second entry in the ``training_data`` tuple is a numpy ndarray
containing 50,000 entries. Those entries are just the digit
values (0...9) for the corresponding images contained in the first
entry of the tuple.
The ``validation_data`` and ``test_data`` are similar, except
each contains only 10,000 images.
This is a nice data format, but for use in neural networks it's
helpful to modify the format of the ``training_data`` a little.
That's done in the wrapper function ``load_data_wrapper()``, see
below.
"""
f = gzip.open('../data/mnist.pkl.gz', 'rb')
training_data, validation_data, test_data = cPickle.load(f)
f.close()
return (training_data, validation_data, test_data)
def load_data_wrapper():
"""Return a tuple containing ``(training_data, validation_data,
test_data)``. Based on ``load_data``, but the format is more
convenient for use in our implementation of neural networks.
In particular, ``training_data`` is a list containing 50,000
2-tuples ``(x, y)``. ``x`` is a 784-dimensional numpy.ndarray
containing the input image. ``y`` is a 10-dimensional
numpy.ndarray representing the unit vector corresponding to the
correct digit for ``x``.
``validation_data`` and ``test_data`` are lists containing 10,000
2-tuples ``(x, y)``. In each case, ``x`` is a 784-dimensional
numpy.ndarry containing the input image, and ``y`` is the
corresponding classification, i.e., the digit values (integers)
corresponding to ``x``.
Obviously, this means we're using slightly different formats for
the training data and the validation / test data. These formats
turn out to be the most convenient for use in our neural network
code."""
tr_d, va_d, te_d = load_data()
training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
training_results = [vectorized_result(y) for y in tr_d[1]]
training_data = zip(training_inputs, training_results)
validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
validation_data = zip(validation_inputs, va_d[1])
test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
test_data = zip(test_inputs, te_d[1])
return (training_data, validation_data, test_data)
def vectorized_result(j):
"""Return a 10-dimensional unit vector with a 1.0 in the jth
position and zeroes elsewhere. This is used to convert a digit
(0...9) into a corresponding desired output from the neural
network."""
e = np.zeros((10, 1))
e[j] = 1.0
return e
Ինչպես վերևում նշել եմ, մեր ծրագիրը ցույց է տալիս բավականին լավ արդյունքներ։ Սակայն ի՞նչ է դա նշանակում։ Ինչպե՞ս է որոշվում լավ կամ վատ արդյունքը։ Օրինակ, բավականին ինֆորմատիվ կլինի եթե կառուցենք պարզ (ոչ նեյրոնային ցանց) հիմքային թեստեր՝ համեմատության համար, որպեսզի հասկանանք, թե ինչ է նշանակում լավ արդյունք ունենալ։ Իհարկե, ամենից պարզ հիմքային թեստը դա պատահականորեն գուշակված թվանշանն է, որը կգուշակի մոտավորապես տաս տոկոս ճշտությամբ։ Հարկ է նշել, որ մեր ալգորիթմը էապես ավելի ճշգրիտ է։
Ի՞նչ կասեք ավելի քիչ տրիվիալ թեստի մասին։ Փորձենք բավականին պարզ գաղափար. դիրարկենք նկարի մգությունը։ Օրինակ, $2$ թվանշանին համապատասխանող նկարը սովորաբար ավելի մուգ կլինի, քան $1$-ին համապատասխանող նկարը, քանի որ ավելի շատ պիքսելներ են սև։ Տես ներքևում պատկերված օրինակը

Օգտագործենք մարզման տվյալները՝ $0, 1, 2,\ldots, 9$ թվանշանների համար միջին մգությունը հաշվելու համար։ Յուրաքանչյուր նկարի համար, կհաշվենք մգությունը, այնուհետև համեմատելով, կգտնենք ամենամոտիկ միջին մգությամբ նկարը, որը կօգտագործենք գուշակման համար։ Դա պարզ պրոցեդուրա է և համապատասխան կոդի իրականացնելը դժվար չէ։ Հետևաբար այն չենք ներկայացնի այս էջում, իսկ հետաքրքրվողների համար այն կարելի է գտնել հետևյալ հղումով GitHub repository Սա պատահական գուշակման համեմատ էական բարելավում է, որի հետևանքով $10,000$-ից $2,225$ թվանշանները ճիշտ են գուշակվում, ինչը նշանակում է $22.25$ տոկոս ճշտություն։
Դժվար չէ գտնել այլ իդեաներ, որոնք հասնում են $20$-ից $50$ տոկոս ճշտության։ Եթե ավելի շատ փորձեք, կարող եք նաև $50$ տոկոսն անցնել։ Սակայն ավելի մեծ ճշտությունների հասնելու համար օգտակար է այլ մեքենայական ուսուցման ալգորիթմների օգտագործումը։ Փորձենք օգտագործել ամենահայտնի ալգորիթմերից մեկը՝ support vector machine կամ SVM։ Եթե ծանոթ չեք SVM-ների հետ, ապա պետք չէ անհանգստանալ, քանի որ մենք կարիք չենք ունենալու հասկանալ, թե SVM-ներն ինչպես են աշխատում։ Դրա փոխարեն կօգտագործենք Python-ի գրադարանը, որը կոչվում է scikit-learn, որը Python-ի պարզ միջերես (interface) է SVM-ների համար, որը հայտնի է որպես LIBSVM։
Եթե գործարկենք scikit-learn-ի SVM դասակարգիչը, օգտագործելով լռելյայն (default) կարգավորումները, ապա կստանանք 10,000-ից 9,435 թեստային նկարների ճիշտ դասակարգում։ (Կոդը հասանելի է այստեղ.) Սա էական բարելավում է՝ համեմատած դասակարգման մեր նախորդ ավելի պարզ մոտեցումների։ SVMի արդյունավետությունը շատ մոտ է մեր նեյրոնային ցանցին, սակայն փոքր-ինչ զիջում է։ Հետագա գլուխներում կներկայացնենք նոր մոտեցումներ, որոնք թույլ են տալիս բարելավել նեյրոնային ցանցերն այնպես, որ իրենց ճշգրտությունն էապես բարձր է SVM-ներից։
Սակայն դա վերջը չէ։ 10,000-ից 9,435 ճիշտ արդյունքը դեռ ստացվում է scikit-learn-ի SVM-ների համար նախատեսված լռելյայն կարգավորումներով։ SVM-ներն ունեն բազմաթիվ պարամետրեր, որոնք կարելի է փոխել և արդյունքն էլ ավելի բարելավել։ Ավելի լավ պարամետրերը կարելի է որոշակի մեխանիզմներով փնտրել, որը այստեղ չենք իրականցնի, սակայն կարող եք հղվել հետևյալ բլոգային գրառմանը, որի հեղինակն է Անդրեաս Մյուլլերը, եթե հետաքրքրված եք ավելին իմանալու։ Մյուլլերը ցույց է տալիս, որ պարամետրերը օպտիմալացնելու որոշակի աշխատանք կատարելուց հետո կարելի է ճշգրտությունը հասցնել մինչև 98.5 տոկոսի։ Այլ կերպ ասած, լավ կարգավորված SVM-ը սխալվում է ամեն 70 թվանշանը մեկ։ Դա բավականին լավ է։ Կարո՞ղ են արդյոք նեյրոնային ցանցերն ավելի արդյունավետ լինել։
Փաստացի, կարող են։ Ներկայումս, լավ նախագծված նեյրոնային ցանցն ավելի ճշգրիտ է, քան մնացած հայտնի MNIST-ի լուծման մեթոդները, այդ թվում նաև SVM-ները։ Ներկայիս (2013) դասակարգման ռեկորդը 10,000-ից 9,979 ճիշտ նկարների ճանաչումն է։ Այդ արդյունքը գրանցվել է Լի Վուանի (Li Wan) , Մաթյու Զեիլերի (Matthew Zeiler), Սիքսին Ժանգի (Sixin Zhang), Յան Լեքունի (Yann LeCun) և Ռոբ Ֆերգյուսի (Rob Fergus) կողմից։ Գրքում հետագայում մենք կտեսնենք իրենց օգտագործած մեթոդների մեծ մասը։ Այդ մակարդակի վրա արտադրողականությունը բավականին մոտ է մարդկանց և վիճելորեն ավելի լավը, քանի որ որոշ MNIST նկարներ նույնիսկ մարդկանց համար են ճանաչման առումով դժվարություն ներկայացնում։
Բավականին տպավորիչ է, որ այնպիսի նկարներն ինչպիսին MNIST-ի նկարներն են, նեյրոնային ցանցերը կարող են 21-ից բացի բոլոր 10,000 նկարները ճիշտ դասակարգեն։ Սովորաբար, ծրագրավորելիս, մենք համոզված ենք, որ MNIST թվանշանների ճանաչման խնդրի պես դժվար խնդիր լուծելիս անհրաժեշտ է դժվար ալգորիթմ։ Սակայն նույնիսկ Վուան և այլոք (Wan et al) հոդվածում նշված նեյրոնային ցանցերը ներգրավում են բավականին պարզ ալգորիթմներ, որի որոշակիորեն ձևափոխված տարբերակին ականատես եղանք այս գլխում։ Ամբողջ բարդությունն ինքնըստինքյան ուսուցանվում է տվյալներից։ Ինչ-որ իմաստով կարելի է ասել, որ մեր ստացած երկու արդյունքների և նրանց, որոնք գրված են բազմաթիվ հոդվածներոմ, կապվում են իրար հետ հետևյալ գաղափարով.
Խորը ուսուցմանն ընդառաջ
Մեր նեյրոնային ցանցի արտադրողականությունը բավականին տպավորիչ է, սակայն միևնույն ժամանակ միստիկ։ Ցանցի կշիռներն ու շեղումները ավտոմատ կերպով են հայտնաբերվել։ Եվ դա նշանակում է, որ մենք չունենք անմիջական բացատրություն, թե ինչպես է ցանցը իրականացնում այն ինչ իրականացնում է։ Կարո՞ղ ենք արդյոք ինչ-որ կերպ հասկանալ մեր ցանցի՝ ձեռագիր թվանշաններ ճանաչելու սկզբունքները։ Եվ, եթե գիտենք այդ սկզբունքները, ապա կարո՞ղ ենք բարելավել արդյունքները։
Ենթադրենք, որ մի քանի տասնամյակ անց նեյրոնային ցանցերը հանգեցնում են Արհեստական Բանականության (ԱԲ)։ Կկարողանա՞նք մենք արդյոք հասկանալ, թե ինչպես է այդպիսի բանականությունն աշխատում։ Կարող է ցանցերը ոչ թափանցիկ լինեն մեզ համար, որի կշիռներն ու շեղումները մենք չենք հասկանա, քանի որ դրանք ուսուցանվել են ավտոմատ կերպով։ Արհեստական Ինտելեկտի ուսումնասիրությունների վաղ ժամանակներում մարդիկ հույս ունեին, որ ԱԻ ստեղծելու ջանքերը միաժամանակ կօգնեին մեզ հասկանալ ինտելեկտի սկզբունքները կամ նույնիսկ մարդկային ուղեղի աշխատանքի գաղտնիքները։ Սակայն կարող է արդյունքում մենք ո'չ ուղեղի աշխատանքը հասկանանք, ո'չ էլ արհեստական ինտելեկտի։
Որպեսզի փորձենք պատասխանել այս հարցերին, առաջարկում եմ վերադառնալ արհեստական նեյրոնների ինտերպրետացիային, որ ես տվել էի այս գլխի սկզբում։ Ենթադրենք, որ մեր նպատակն է որոշել արդյո՞ք նկարում մարդկային դեմք է, թե ոչ.
Credits: 1. Ester Inbar. 2. Unknown. 3. NASA, ESA, G. Illingworth, D. Magee, and P. Oesch (University of California, Santa Cruz), R. Bouwens (Leiden University), and the HUDF09 Team. Click on the images for more details.
Այս խնդրին կարող ենք մոտենալ այնպես ինչպես ձեռագրերի ճանաչման խնդրին՝ օգտագործելով նկարի պիքսելները որպես նեյրոնային ցանցի մուտք այնպես, որ նեյրոնային ցանցն ունենա մեկ ելքային նեյրոն, որը ցույց կտա կամ «այո, սա դեմք է» կամ «ոչ, սա դեմք չէ»։
Ենթադրենք, որ վարվում ենք հենց այդպես, սակայն այս դեպքում ուսուցման ալգորիթմ չենք օգտագործում։ Փոխարենը, ցանցը կձևավորենք ձեռքով՝ ընտրելով համապատասխան կշիռերն ու շեղումները։ Իսկ ինչպե՞ս կիրականացնեինք դա։ Ժամանակավորապես մոռանալով նեյրոնային ցանցերի մասին, կարող ենք խնդիրը բաժանել ենթախնդիրների. օրինակ նկարի ձախ վերևի անկյունում գոյություն ունի՞ աչք։ Ունի այն արդյոք աչք աջ վերևի անկյունում։ Արդյո՞ք այն քիթ ունի միջնամասում։ Արդյո՞ք այն ունի բերան միջնամասից ներքև գտնվող մասում և այլն …
Եթե այս հարցերից որոշների պատասխանը «այո» է կամ նույնիսկ «հավանաբար այո», ապա մենք կեզրակացնեինք, որ նկարն ամենայն հավանականությամբ դեմք է։ Եվ հակառակը, եթե այս հարցերի մեծամասնության պատասխանը «ոչ» է, ապա նկարն ամենայն հավանականությամբ դեմք չէ։
Իհարկե, սա բավականին կոշտ մեթոդ է և ունի բազում խնդիրներ։ Ճաղատ մարդիկ, օրինակ, մազեր չունեն։ Կարող է պատահել, որ դեմքը մասնակի է երևում կամ անկյան տակ է, ինչի պատճառով որոշ դիմային մասեր տեսանելի չլինեն։ Սակայն, եթե կարողանանք լուծել ենթախնդիրները նեյրոնային ցանցերի միջոցով, ապա հավանաբար կարող ենք կառուցել դեմքի ճամաչման նեյրոնային ցանց՝ միավորելով ենթախնդիրների նեյրոնային ցանցերը։ Ահա հնարավոր նախագիծ, որտեղ ուղղանկյուններով նշված են ենթացանցերը։ Նկատենք, որ սա չենք դիտարկում որպես դեմքերի ճանաչման ռեալիստիկ մեթոդ, այլ փորձում ենք ձեռք բերել ինտուցիա այն մասին, թե ինչպես են ցանցերն աշխատում։ Ահա այդ արխիտեկտուրան.
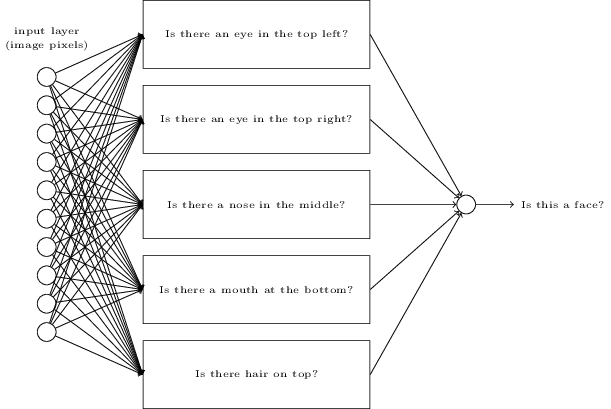
Հնարավոր է նաև, որ ենթացանցերը իրենց հերթին բաժանված լինեն ենթամասերի։ Ենթադրենք, որ դիտարկում ենք հետևյալ հարցը՝ «Արդյո՞ք ձախ վերևի անկյունում աչք կա»։ Սա կարող է մասնատվել այնպիսի հարցերի, ինչպիսիք են «Արդյո՞ք ունք կա», «Արդյո՞ք թարթիչներ կան» և այլն։ Իհարկե այս հարցերը պետք է պարունակեն նաև դիրքային ինֆորմացիա. «Արդյո՞ք ունքը ձախ վերևում է և թարթիչներից վերև և նմանատիպ այլ հարցեր, սակայն չբարդացնենք։ «Արդյոք ձախ վերևում ունք կա» հարցը արդեն կարելի է մասնատել։
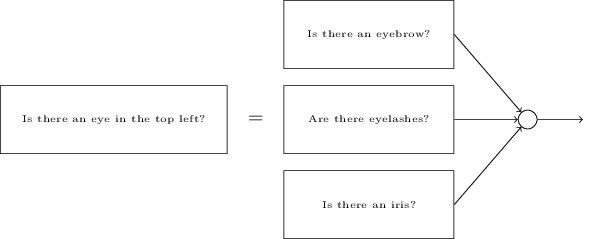
Այդ հարցերը նույնպես հնարավոր է մասերի բաժանել բազմաթիվ շերտերով։ Այսպիսով, մենք կաշխատենք այնպիսի ենթացանցերի հետ, որոնք պատասխանում են այնպիսի պարզ հարցերի, որոնց կարելի է պատասխանել մեկ պիքսելի մակարդակով։ Այդ հարցերը օրինակ կարող են լինել հատուկ տեղամասերում պարզագույն ուրվագծերի ներկայության կամ բացակայության մասին։ Այդպիսի հարցերին կարող են պատասխանել մեկական նեյրոններ, որոնք կապված են նկարի պիքսելներին։
Վերջնական արդյունքը դա մի ցանց է, որն այնպիսի բարդ հարցը ինչպիսին է «Արդյո՞ք նկարում դեմք է պատկերված» բաժանում է բազմաթիվ շատ փոքր հարցերի, որոնց կարելի է պատասխանել մեկ պիքսելի մակարդակով։ Սա իրականացվում է բազմաթիվ շերտերի միջոցով, որի սկզբնական շերտերը պատասխանում են տրիվիալ հարցերի տարատեսակ ուրվագծերի մասին, իսկ վերին շերտերն արդեն կազմում են ավելի կոմպլեքս և աբստրակտ կոնցեպտների մասին հարցերին պատասխանող հիերարխիայի գագաթներ։ Այն ցանցերը, որոնք ունեն նմանատիպ բազմաշերտ կառուցվածք կազմված երկու և ավել շերտերից կոչվում են խորը նեյրոնային ցանցեր (deep neural networks)
Իհարկե մենք դեռ չենք քննարկել, թե ինչպես կարելի է իրականացնել այդպիսի ռեկուրսիվ կազմալուծումը ենթացանցերի։ Անշուշտ ցանցի կշիռներն ու շեղումները ձեռքով կառուցելը պրակտիկ չէ։ Իհարկե, մենք կուզենայինք օգտագործել այնպիսի ուսուցման ալգորիթմներ, որ ցանցն ավտոմատ կերպով սովորի կշիռներն ու շեղումները, հետևաբար նաև կոնցեպտների հիերարխիան՝ մարզման տվյալներից։ 1980-ականներին և 1990-ականներին հետազոտողները փորձել են մարզել խորը ցանցերը՝ օգտագործելով ստոկաստիկ գրադիենտային վայրէջք և հետադարձ տարածում։ Դժբախտաբար, բացի որոշ կառուցվածքներից ուրիշ էական հաջողություն չի գրանցվել։ Ցանցը կսովորեր, սակայն բավականին դանդաղ և հիմնականում այնքան դանդաղ, որ պրակտիկորեն հնարավոր չէր օգտագործել։
2006 թվականից սկսած որոշակի տեխնիկաների խումբ է կառուցվել, որ հնարավորություն է տալիս խորը նեյրոնային ցանցերին սովորել։ Այս խորը ուսուցման տեխնիկաները հիմնված են ստոկաստիկ գրադիենտային վայրէջքի, հետադարձ տարածման և այլ ուրիշ նոր գաղափարների վրա։ Այս մոտեցումները հնարավորություն տվեցին ավելի խորը, մեծ և լայն ցանցեր մարզել - մարդիկ այժմ հեշտությամբ կարողանում են մարզել 5-ից 10 թաքնված շերտերով նեյրոնային ցանցեր։ Եվ պարզվում է, որ այդպիսի ցանցերն ավելի լավ արտադրողականություն ունեն, քան համեմատաբար սաղր ցանցերը, օրինակ մի թաքնված շերտով նեյրոնային ցանցերը։ Պատճառն, իհարկե, այն է, որ խորը նեյրոնային ցանցերը կարողանում են կառուցել կոմպլեքս կոնցեպտների հիերարխիա։ Այն որոշ չափով նման է նրան, որ հիմնական ծրագրավորման լեզուները օգտագործում են մոդուլյար նախագծում և աբստրակցիայի այնպիսի մեխանիզմներ, որ հնարավորություն է տալիս ստեղծել կոմպլեքս ծրագրեր։ Խորը ցանցերը սաղր ցանցերին համեմատելը նման է ֆունկցիայի կանչի հնարավորությամբ ծրագրավորման լեզվի համեմատությանը մի ծրագրավորման լեզվի, որը չունի այդ հնարավորությունը։ Նեյրոնային ցանցերում աբստրակցիան այլ տեսք ունի համեմատած ծրագրավորման լեզուների, սակայն այն հավասարապես կարևոր է։